No filme Oppenheimer, há uma cena onde os físicos de Los Alamos calculam a quantidade de urânio enriquecido necessária para se fazer uma bomba nuclear. A pergunta que quero responder aqui é: Como chegaram neste valor?
Para isso, vamos estudar a física da difusão de neutrons em um material fissionável (capaz de fazer fissão nuclear). Primeiramente devemos nos perguntar que tipo de reações ocorrem com um neutron que viaja dentro de um material fissionável como o urânio. Bem, o neutron tem carga elétrica nula, o que significa que ele não tem sua trajetória desviada pelo campo eletromagnético dos átomos ao seu redor. Isto significa que o neutron só tem sua trajetória alterada se uma das duas coisas ocorrerem:
- O neutron “colide” com o núcleo atômico e tem sua trajetória alterada
- O neutron é absorvido pelo núcleo atômico e deixa de existir
Caso o cenário 2 ocorra, há duas possibilidades subsequentes
2.1. O átomo sofre fissão nuclear, dividindo seu núcleo e liberando mais neutrons no processo
2.2 O átomo não sofre fissão nuclear e o neutron é perdido, isto é, ele para de viajar pelo material e não contribui mais para a quantidade de neutrons livres no material.
O transporte de qualquer quantidade através de um meio obedece a chamada equação da continuidade:
\[\begin{align} \frac{\partial N}{\partial t} + \nabla \cdot J = 0 \end{align}\]Onde aqui $N$ representa a quantidade de partículas e $J$ representa a corrente de transporte destas partículas. Esta equação é aplicável para transporte de cargas elétricas, massa, energia, fluídos, etc. Entretanto, a forma atual da equação de continuidade implica que o quantidade total de partículas $N$ é conservada, ou seja, ela não muda conforme o tempo passa. No nosso caso, cada reação de fissão nuclear cria novos neutrons, bem como reações de absorção de neutrons os elimina. É importante aqui dizer que os únicos neutrons que estamos considerando em $N$ são os neutrons livres que estão viajando pelo material, portanto uma vez que um neutron deixa de ser livre e é capturado por um núcleo, ele deixa de contar para $N$. Assim, precisamos que nossa equação não seja igual a zero, mas sim ao balanço de neutros criados e eliminados.
\[\begin{align} \frac{\partial N}{\partial t} + \nabla \cdot J = S_+ - S_- \end{align}\]Aqui podemos agora ver como o termo de corrente $\nabla \cdot J$ pode ser reescrito. A movimentação dos neutrons é puramente estocástica e aleatória. Um neutron viaja em linha reta até interagir com um núcleo atômico de forma a alterar sua rota. Podemos descrever esse processo como um processo de difusão simples, onde a corrente neutrônica flui de acordo com o gradiente da concentração de neutrons no meio, de onde há maior densidade para onde há menor densidade. Portanto
\[\begin{align} \nonumber & \frac{\partial N}{\partial t} + \nabla \left( -D \nabla N \right) = S_+ - S_- \Rightarrow \\ \nonumber & \frac{\partial N}{\partial t} - D \nabla^2 N = S_+ - S_- \Rightarrow \\ \nonumber & \frac{\partial N}{\partial t} = D \nabla^2 N + S_+ - S_- . \end{align}\]Legal, mas ainda não conseguimos resolver isso… primeiro o que é a difusividade $D$? Em segundo, quem são os termos de criação de neutrons $S_+$ e absorção de neutrons $S_-$?
O termo de criação pode ser descrito como uma taxa de criação de neutrons devido à fissão nuclear. Esta taxa é dada em termos da quantidade média de neutrons produzidos por reação de fissão $\nu$, o tempo médio entre fissões nucleares $\tau$ e a quantidade de neutrons livres no material $N$
\[\begin{align} \nonumber & S_+ = \nu \frac{N}{\tau} \end{align}\]Note aqui que $\tau$ está intimamente relacionado com a probabilidade de ocorrência de fissões nucleares no material, átomos mais estáveis são muito menos suscetíveis à fissão nuclear, portanto $\tau$ tende a ser muito maior. Agora, uma vez que cada fissão nuclear absorve um neutron livre, os neutrons livres são removidos do meio com uma taxa proporcional à ocorrência de fissões nucleares
\[\begin{align} \nonumber & S_- = \frac{N}{\tau} \end{align}\]Já a difusividade $D$ é dada em termos da velocidade média dos neutrons livres $\left \langle v \right \rangle$ e o livre caminho médio para ocorrência de qualquer tipo de interação neutron-núcleo $\lambda_t$, aqui denominada como livre caminho médio total
\[\begin{align} \nonumber & D = \frac{1}{3} \lambda_t \left \langle v \right \rangle \end{align}\]A velocidade média de neutrons por sua vez pode ser determinada em termos do livre caminho médio para ocorrência de fissão nuclear, divido pelo tempo médio até ocorrência de fissão
\[\begin{align} \nonumber & \left \langle v \right \rangle = \frac{\lambda_f}{\tau} \end{align}\]Já o livre caminho médio por si próprio é uma quantia que depende da massa atômica $A$ dos átomos que compõe o material, a densidade do material $\rho$, a constante de avogrado $N_A$ e a sessão de choque de interação
\[\begin{align} \nonumber & \lambda_f = \frac{A}{\rho N_A \sigma_f}, \end{align}\]sendo a única diferença entre o livre caminho médio total e o de fissão, a sessão de choque de interação. No primeiro, estamos usamos a sessão de choque total, considerando reações de fissão e de espalhamento elástico do neutron nos átomos $\sigma_t = \sigma_f + \sigma_e$, enquanto que no segundo apenas usamos $\sigma_f$. Utilizando estas descrições chegamos finalmente à
\[\begin{align} \nonumber & \frac{\partial N}{\partial t} = \frac{\nu - 1}{\tau} N + \frac{1}{3}\lambda_t \left \langle v \right \rangle \nabla^2 N \end{align}\] \[\begin{align} \nonumber & \frac{\partial N}{\partial t} = \frac{\nu - 1}{\tau} N + \frac{\lambda_t \lambda_f}{3 \tau} \nabla^2 N \end{align}\]Está é a equação de difusão de neutrons. Encontrar a massa crítica para uma reação nuclear envolve o processo de solução desta equação. A princípio podemos achar difícil resolver esta equação por ser uma equação diferencial parcial, onde $N$ é uma função que depende da posição espacial $\vec{x}$ e o tempo $t$. Entretanto, com um simples truque matemático podemos simplificar nossa situação. Suponhamos que nossa solução é separável, isto é, podemos dizer que $N(\vec{x},t)$ é uma função que envolve a multiplicação de uma função que descreve apenas a parte espacial com uma outra função que descreve apenas a parte temporal, $N(\vec{x},t) = f(\vec{x})g(t)$. Este é conhecido como o método da separação de variáveis.
E como sabemos que esta suposição está correta? Nós testamos. Se a solução realmente assumir uma forma como esta, ao substituirmos esta tentativa de separação de soluções na equação diferencial parcial, iremos acabar com duas equações separadas, uma para o espaço e outra para o tempo.
\[\begin{align} \nonumber & \frac{\partial (fg)}{\partial t} = \frac{\nu - 1}{\tau} (fg) + \frac{\lambda_t \lambda_f}{3 \tau} \nabla^2 (fg) \Rightarrow \\ \nonumber & f\frac{\partial g}{\partial t} = \frac{\nu - 1}{\tau} fg + \frac{\lambda_t \lambda_f}{3 \tau} (\nabla^2 f)g \Rightarrow \\ & \frac{1}{g}\frac{\partial g}{\partial t} = \frac{\nu - 1}{\tau} + \frac{\lambda_t \lambda_f}{3 \tau} \frac{\nabla^2 f}{f} \end{align}\]Nesta última equação, podemos notar que o lado esquerdo da equação envolve apenas a função temporal, enquanto que o lado direito envolve apenas a função espacial. A única forma de que uma equação em uma variável seja igual à equação descrita por outra variável, é caso ambas sejam iguais à mesma constante $K$. Porém, já que o lado esquerdo da equação tem unidades de 1/tempo, $K$ também é uma constante com unidades de 1/tempo. Vamos reescrever $K$ como $\nu’/\tau$, apenas para que assim a constante misteriosa $\nu’$ seja adimensional.
\[\begin{align} \nonumber & \frac{1}{g}\frac{\partial g}{\partial t} = \frac{\nu - 1}{\tau} + \frac{\lambda_t \lambda_f}{3 \tau} \frac{\nabla^2 f}{f} = K = \frac{\nu'}{\tau} \end{align}\]Começamos com uma equação diferencial parcial e terminamos com duas equações diferenciais ordinárias! Está é a magia do método da separação de variáveis, trocamos a complexidade de uma única equação por um número maior de equações mais simples.
\[\begin{align} \nonumber & \frac{1}{g}\frac{\partial g}{\partial t} = \frac{\nu'}{\tau} \\ \nonumber & \frac{\nu - 1}{\tau} + \frac{\lambda_t \lambda_f}{3 \tau} \frac{\nabla^2 f}{f} = \frac{\nu'}{\tau} \end{align}\]Equação temporal
Vejamos a solução da nossa equação temporal. Ela é uma equação diferencial simples e razoavelmente comum, cuja solução é bem conhecida como uma exponencial
\[\begin{align} \nonumber & \frac{\partial g}{\partial t} = \frac{\nu'}{\tau}g \Rightarrow \\ & g(t) = A e^{\nu' t/\tau}. \end{align}\]Nesta exponencial, se $\nu’ > 1$, $g(t)$ cresce exponencialmente, o que irá resultar em um crescimento exponencial de $N$ (chamada reação supercrítica), já se $\nu’ < 1$, então $g(t)$ decai exponencialmente (reação subcrítica). Ou seja, para que a quantidade de neutrons gerados aumente exponencialmente, levando à uma explosão nuclear, preciamos que $\nu’$ seja maior que $1$.
Equação espacial
A equação espacial pode a principio parecer mais difícil, mas podemos reorganizar as constantes todas de um lado e renomea-las para manter uma notação mais compacta. Com isso, vemos que a equação diferencial é na verdade bem simples, o termo que pode introduzir dificuldade para nós é justamente o laplaciano $\nabla^2$
\[\begin{align} \nonumber & \frac{\lambda_t \lambda_f}{3 \tau} \frac{\nabla^2 f}{f} = -\frac{\nu - 1 - \nu'}{\tau} \Rightarrow \\ \nonumber & \frac{\lambda_t \lambda_f}{3 \tau} \nabla^2 f = -f \left(\frac{\nu - 1 - \nu'}{\tau}\right) \Rightarrow \\ \nonumber & \nabla^2 f = -f \underbrace{\left[\frac{3(\nu - 1 - \nu')}{\lambda_t \lambda_f}\right]}_{\kappa^2} \Rightarrow \\ \nonumber & \nabla^2 f = -f \kappa^2 \end{align}\]E aqui a forma do laplaciano depende do sistema de coordenadas que usaremos para descrever a posição espacial dos neutrons. Nosso sistema de coordenadas depende da geometria escolhida para o núcleo de material fissionável. A escolha mais simples é uma esfera homogênea de material, de forma que o formato esférico proporcione uma simetria em todas as direções, como resultado a densidade de neutrons passa a ser descrita por uma única variável, que é a distância radial com relação ao núcleo da esfera $N(\vec{x}) = N(r)$, assim
\[\begin{align} \nonumber \nabla^2 = \frac{1}{r^2}\frac{d}{dr}\left(r^2 \frac{d}{dr} \right) \end{align}\]E novamente parece que teremos uma equação difícil em nossas mãos, ao aplicarmos o laplaciano em nossa equação teremos termos envolvendo as primeiras e segundas derivadas da função $f$, isso irá resultar em uma equação diferencial de segunda ordem. Isso não impossibilita a solução, mas sem dúvida a complica. Felizmente, se fizermos a mudança de variáveis $f = u/r$ e passarmos a escrever a equação em termos da função $u$, ao invés de $f$, notaremos que o laplaciano se reduz a
\[\begin{align} \nonumber \nabla^2 f = \frac{1}{r}\frac{d^2 u}{dr^2}, \end{align}\]e assim a equação diferencial espacial se torna
\[\begin{align} \nonumber \frac{d^2 u}{dr^2} = - \kappa^2 u \end{align}\]que assim como a equação temporal, é uma equação diferencial comumente conhecida, cuja solução é uma soma de senos e cossenos (você pode resolver manualmente através do método da equação característica, onde verá que a exponencial resultante é complexa. Utilizando a identidade de Euler, o resultado surgirá como senos e cossenos)
\[\begin{align} \nonumber & u(r) = B \cos(\kappa r) + C \sin(\kappa r) \Rightarrow \\ \nonumber & f(r) = B \frac{\cos(\kappa r)}{r} + C \frac{\sin(\kappa r)}{r} \end{align}\]Chegamos finalmente na solução final da equação de difusão de neutrons
\[\begin{align} N(r,t) = A e^{\nu' t/\tau} \left[B \frac{\cos(\kappa r)}{r} + C \frac{\sin(\kappa r)}{r}\right], \end{align}\]só que ela não nos ajuda a determinar grandezas físicas uma vez que não sabemos quais são as constantes $\nu’$, $A$ e $B$. Para determina-las aplicamos as condições de contorno ao nosso problema. Ou seja, no momento temos uma solução matemática e veremos qual é a solução que possui significado físico.
Condições de contorno
- A primeira condição de contorno é que a densidade de neutrons deve ser finita no núcleo da esfera a todo instante, ou seja $\lim_{r \rightarrow 0} N(r,t) \neq \infty$. Vejamos a nossa solução
Logo $B = 0$ para garantir que a densidade $N(r,t)$ continue finita.
- Em seguida, também pensando no realismo físico, definimos que em $t=0$, a quantidade inicial de neutrons livres no centro é $N_0 \neq 0$. Com isso encontramos que
E assim descobrimos mais algumas constantes, chegando na solução
\[\begin{align} \nonumber & N(r,t) = N_0 e^{\nu' t/\tau} \frac{\sin(\kappa r)}{\kappa r} \end{align}\]- Finalmente, a terceira condição de contorno é de que nenhum neutron escapa da esfera. Está condição é a mais debatível das 3, uma vez que alguns neutrons podem sim escapar do material fissionável. Entretanto, o material pode ser encapsulado com um material cuja sessão de choque para a reflexão de neutrons seja alta, de forma que a quantia de neutrons que escapa pelo material que veda a esfera de fissão é irrisória, podendo ser desconsiderada. No final das contas queremos que $N(R,t) = 0$, sendo $R$ o raio da esfera
A solução mais simples para que isso seja verdade é que $\kappa R = \pi$. Mas pela definição de $\kappa$, tinhamos
\[\begin{align} \nonumber \kappa^2 = \left[\frac{3(\nu - 1 - \nu')}{\lambda_t \lambda_f}\right] = \frac{\pi^2}{R^2} \end{align}\]isolando $\nu’$, encontramos
\[\begin{align} \nonumber \nu' = (\nu - 1) - \frac{\pi^2 \lambda_f \lambda_t}{3 R^2} \end{align}\]Finalmente chegamos à solução final
\[\begin{align} \nonumber & N(r,t) = N_0 R e^{\nu' t/\tau} \frac{\sin(\pi r / R)}{\pi r} \end{align}\]com $\nu’$ dado pela equação anterior.
| constante | interpretação | valor $\mathrm{U}^{235}$ | valor $\mathrm{Pu}^{239}$ |
|---|---|---|---|
| $\tau$ | Tempo médio entre fissões | 16.5 ns | – |
| $\nu$ | Quantidade média de neutrons liberados por fissão | 2.6 | 3.17 |
| $\lambda_f$ | Livre caminho médio de fissão | 16.89 cm | 14.14 cm |
| $\lambda_t$ | Livre caminho médio total | 3.596 cm | 2.87 cm |
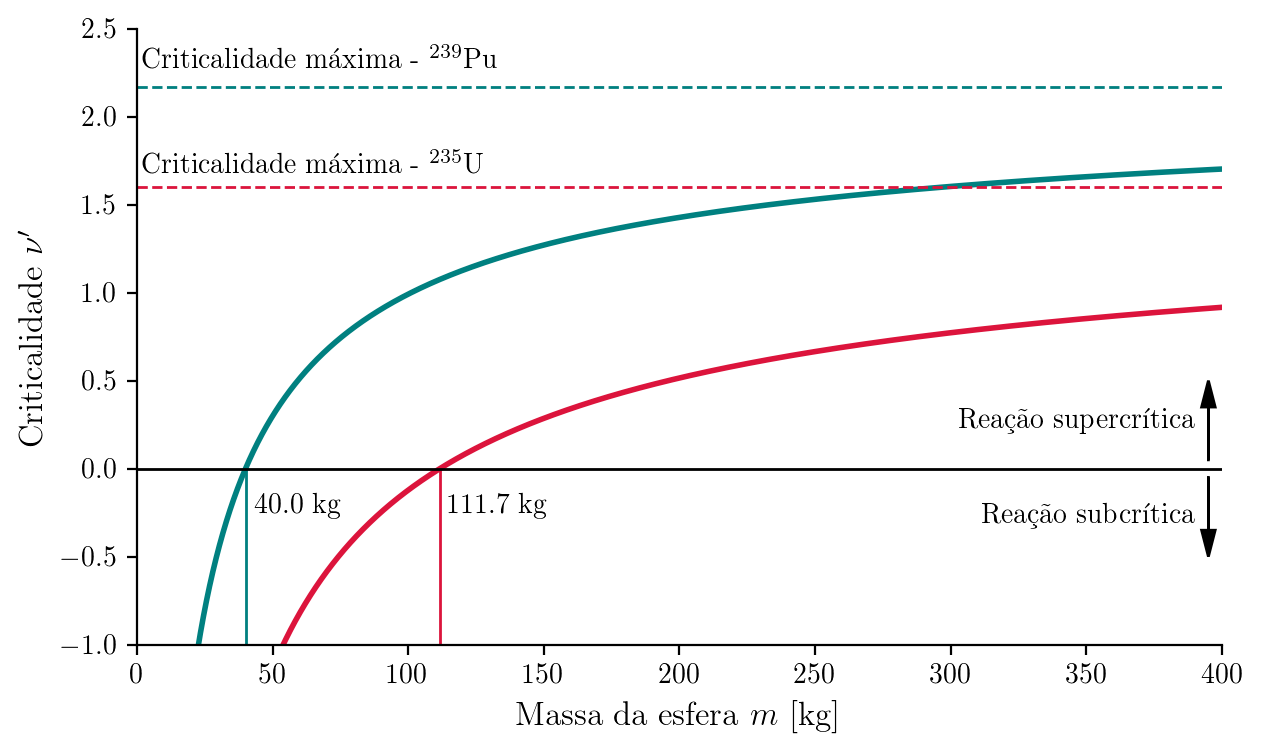
Colocando $\nu’ = 0$
\[\begin{align} \nonumber & R_c = \pi \sqrt{\frac{\lambda_t \lambda_f}{3(\nu-1)}} = \frac{\pi A}{\rho N_A} \sqrt{\frac{1}{3 \sigma_t \sigma_f (\nu-1)}} \end{align}\]Se $M = 4 \pi \rho R^3 / 3$, temos que a massa crítcia $M_c$ é dada por
\[\begin{align} \nonumber & M_c = \frac{4 \pi^4 A^3}{3 \rho^2 N_A^3} \left[{\frac{1}{3 \sigma_t \sigma_f (\nu-1)}}\right]^{3/2} \end{align}\]