Se você já estudou dinâmica de populações, seja em ecologia ou epidemiologia, você já deve ter se deparado com o modelo logístico. Um dos primeiros modelos apresentados na descrição de um crescimento populacional. E assim como eu, você provavelmente se deparou com uma equação diferencial nesse formato
\[\begin{align} \frac{\mathrm{d}N}{\mathrm{d}t} = rN \left(1 - \frac{N}{k} \right) \end{align}\]onde $k$ é a capacidade de suporte da população; isto é, o valor máximo que ela pode atingir, $r$ é a taxa de crescimento e $N$ é o valor da população em um certo instante de tempo. O que essa equação nos diz é que a taxa de variação no tempo, de uma população sujeita apenas à limitação de recursos (sem sofrer predação ou outras interações com outras populações) cresce rapidamente mas tende a se estabilizar em um valor máximo, ditado pelas condições ambientais.
Mas ok, e de onde essa equação veio? Você talvez tenha visto uma construção que começa a partir de um crescimento exponencial, e então adiciona a limitação por recursos para chegar ao modelo logístico. Eu não gosto muito dessa derivação (aos mais preciosistas que queiram argumentar se isso é ou não uma derivação, estou simplificando a linguagem aqui para tentar elaborar algo mais coloquial), pois ela não nos mostra de forma clara que tipo de premissas assumimos a respeito dos indivíduos que compõe essa população. Para isso, precisamos montar essa equação, partindo da dinâmica individual. Esté é meu objetivo aqui.
A transição entre a dinâmica de indivíduos para o comportamento de população é para mim um fenômeno extraordinário. Talvez pelo meu histórico como um físico, eu tenha me apegado e encontrado uma certa beleza em observar descrições individuais e simples resultar em comportamentos macroscópicos complexos. Para os leitores físicos, eu tendo a pensar na transição entre o formalismo de operadores da mecânica quântica para o formalismo padrão da mecânica clássica, ao tomarmos a média dos operadores em um sistema de muitas partículas. Aqui a coisa não será tão diferente, matematicamente falando.
Mas chega de enrolação, vamos lá. Aqui irei supor uma dinâmica que, a primeira vista, pode enfurecer muitos dos meus amigos biológos, mas peço paciência pois tentarei justificar as suposições aqui feitas. A primeira suposição é a de que a única interação que ocorre é entre indivíduos consumidores e seus recursos, ou seja, estamos ignorando a predação, competição interespecífica e até mesmo a reprodução sexuada dentro da própria população. É claro que este é um cenário longe da realidade, mas temos que começar em algum lugar. Foi ignorando a resistência do ar que Galileu começou a descrever o movimento dos corpos.
Como consequência da primeira suposição, a segunda suposição é que os indivíduos se reproduzem assexuadamente. Não é atoa que as observações que melhor batem com a dinâmica logística são aquelas feitas em laboratório com microorganismos (um dos primeiros experimentos avaliando o crescimento logístico foi em 1934 por G. F. Gause, Struggle for Existence).
Uma vez que estamos interessados apenas em descrever a dinâmica dos consumidores do recurso, focaremos neles. Sendo assim, em um certo instante de tempo, 4 coisas diferentes podem ocorrer:
- Um indivíduo $X$ pode se reproduzir assexuadamente resultando então em $X + X$. Representamos isso da forma
- Um indvíduo $X$ pode morrer por causas naturais (velhice, fome, doença, etc).
- Dois indivíduos podem “brigar” por um recurso ou até mesmo por espaço, de forma que apenas um deles sobreviva
- Nada acontecer
Aqui $b$ é a taxa com a qual indivíduos se reproduzem. Está taxa é proporcional à quantidade de recurso disponível para cada indivíduo e a probabilidade de um indivíduo encontrar recurso. Mais tarde discutirei mais a respeito destas taxas. $d$ é a taxa de morte por causas naturais e $\alpha$ a taxa com a qual indivíduos morrem devido à competição.
Vale notar aqui que deixamos aqui implícita a 3ª premissa do modelo: Não há mutações e as taxas de para cada processo não dependem das características do indivído, ou seja, todos os indivíduos são iguais. Em termos ecológicos, podemos dizer que todos os indivíduos possuem a mesma aptidão (aqui estou usando aptidão como uma tradução para o fitness).
As coisas agora ficarão mais matemáticas ![]() . Afim de obter uma descrição populacional destes indivíduos, nos perguntamos qual é a probabilidade de que, entre os instantes de tempo $t$ e $t + \Delta t$, observemos $N$ indivíduos nesta população. De forma mais “física” dizemos que o sistema está no estado $N$. Alguns físicos talvez possam pensar algo como “pera aê
. Afim de obter uma descrição populacional destes indivíduos, nos perguntamos qual é a probabilidade de que, entre os instantes de tempo $t$ e $t + \Delta t$, observemos $N$ indivíduos nesta população. De forma mais “física” dizemos que o sistema está no estado $N$. Alguns físicos talvez possam pensar algo como “pera aê ![]() isso não parece com a terminologia que se usa para descrever o estado de um sistema em mecânica quântica?” e quem pensou isso está completamente certo. Se você não pensou, tudo bem a vida já tem coisa demais para pensarmos.
isso não parece com a terminologia que se usa para descrever o estado de um sistema em mecânica quântica?” e quem pensou isso está completamente certo. Se você não pensou, tudo bem a vida já tem coisa demais para pensarmos.
Bem, é claro que muitas coisas podem ocorrer em um intervalo de tempo $\Delta t$, porém algumas são mais prováveis do que outras. Como assim? Bem, vejamos… se $b$, $d$ e $\alpha$ são taxas para a ocorrência de cada cenário, a probabilidade de que cada um deles sozinho ocorra em um certo intervalo $\Delta t$ é dada pela quantidade de indivíduos no início deste intervalo, multiplicada pela taxa de ocorrência (também chamada de taxa de transição) e o intervalo de tempo em questão. Por exemplo, a chance de que alguém se reproduza durante $\Delta t$ e a população vá para o valor $N$ é $(N-1) b \Delta t$. Se você parar para pensar, faz sentido que quanto mais indivíduos na população, maior a chance de algum deles se reproduzir, assim como essa chance também deve aumentar quanto maior for o intervalo $\Delta t$, ou maior for a taxa $b$.
Entretanto, para quem a população saia de $N-1$ indivíduos em $t$ e vá para $N$ indivíduos em $t + \Delta t$, devido apenas à reprodução, somente um indivíduo deve se reproduzir. Sendo assim, a chance $P$ de que isso ocorra se resume a probabilidade de um indivíduo se reproduzir enquanto que todos os outros não se reproduzam. Se a chance de reprodução de um único indivíduo é $b \Delta t$, a chance de que um indivíduo não se reproduza é $1 - b \Delta t$. Portanto
\[\begin{align} P_{N-1 \rightarrow N}^{r} &= \underbrace{(N-1)b \Delta t}_{\text{um dos N-1 se reproduz}} \times \overbrace{\left(1 - b \Delta t \right)^{N-2}}^{\text{todos os outros N-2 não}} \end{align}\]por exemplo, se queremos a chance de que através da reprodução, a população chege em $N = 4$ em $t + \Delta t$, teremos então
\[\begin{align} P_{3 \rightarrow 4}^{r} &= 3b \Delta t \times \left(1 - b \Delta t \right)^{2} = \\ \nonumber & = 3b\Delta t \times \left(1 - 2b\Delta t + b^2\Delta t^2 \right) = \\ \nonumber & = 3b\Delta t - 6b^2 \left(\Delta t \right)^2 + 3b^3 \left(\Delta t \right)^3 \end{align}\]e este polinômio de $\Delta t$ aumenta cada vez mais conforme $N$ aumenta. Ótimo, parece que temos uma descrição completamente intratável, como alguém esperaria que nós iremos calcular um polinômio desses em um caso onde $N = 10000$ por exemplo?
Para a nossa felicidade, as maravilhas do cálculo nos salvarão. Mas deixarei para invocar nosso herói mais tarde.
E você pode estar pensando “ora, ora, ora, mas você mesmo disse que muitas coisas podem ocorrer neste intervalo de tempo. E se dois indivíduos se reproduzirem?”. Vamos ver exatamente isso agora. Nesse caso, a população precisaria estar, no instante de tempo $t$, com $N-2$ indivíduos e dois deles precisariam se reproduzir (lembrando aqui que queremos apenas considerar eventos que contribuam para que em $t + \Delta t$ a população tenha $N$ indivíduos). Após a primeira reprodução, seria necessária uma segunda, agora com a população em $N-1$ e um intervalo de tempo restante $\Delta t’ < \Delta t$. Assim, podemos dizer que a probabilidade $P$ de que o sistema saia do estado $N -2 $ e vá para $N$ durante $\Delta t$, apenas por reprodução, é
\[\begin{align} P_{N-2 \rightarrow N}^{r} = \underbrace{(N-2)b \Delta t}_{\text{1ª reprodução}} \overbrace{(N-1) b \Delta t'}^{\text{2ª reprodução}} \underbrace{\left(1 - b \Delta t\right)^{N-3}}_{\text{Ninguém mais reproduz}}. \end{align}\]Caso a reprodução seja simultânea $\Delta t’ = \Delta t$ e a população em ambas as reproduções é a mesma, portanto
\[\begin{align} P_{N-2 \rightarrow N}^{r} = \left[(N-2) b \Delta t \right]^2 \left(1 - b \Delta t\right)^{N-3} . \end{align}\]Podemos brincar com diversos cenários e inumeras formas nas quais a população pode estar em um nível $N’ \neq N$ e chegar em $N$ entre os momentos $t$ e $t + \Delta t$.
Aqui é importante notar que para calcular estas probabilidades eu tive que introduzir sutilmente a 4ª premissa de que os eventos são independentes; ou seja, o que ocorre com seu vizinho pouco importa a você.
Note que para qualquer evento neste intervalo, há termos na probabilidade que dependem de $\left(\Delta t\right)^m$. Uma vez que iremos considerar intervalos de tempo pequenos, de forma que $\Delta t \rightarrow 0$, probabilidades com maiores potências de $\Delta t$ se tornam cada vez menos prováveis. Por exemplo, no caso de uma única reprodução, para atingir uma população de $N = 4$, calculamos a probabilidade desse evento como sendo a equação
\[\begin{align} P_{3 \rightarrow 4}^{r} = 3b\Delta t - 6b^2 \left(\Delta t \right)^2 + 3b^3 \left(\Delta t \right)^3 \end{align}\]e a chance de que duas reproduções ocorram é dada por
\[\begin{align} P_{2 \rightarrow 4}^{r} &= 4b^2\left(\Delta t \right)^2 \left(1 - b \Delta t\right) = \\ \nonumber & = 4b^2\left(\Delta t \right)^2 - 4b^3\left(\Delta t \right)^3 \end{align}\]Note que apenas o evento de uma única reprodução possui uma contribuição de $\Delta t$. Isso significa que conforme $\Delta t \rightarrow 0$, este termo fica muito maior do que todos os demais e então $P_{3 \rightarrow 4}^{r} \gg P_{2 \rightarrow 4}^{r}$. Ou seja, se olharmos para um intervalo de tempo curto o suficiente, a chance de que dois eventos ocorram se torna muito menor do que apenas um deles ocorrer.
Antes de continuar, vamos parar um pouco para pensar sobre isso. Se considerarmos um intervalo de tempo de 1 mês, o que você acha mais provável, que apenas uma criança nasça no Brasil durante esse intervalo, ou que muitas crianças nasçam? Certamente em um mês, é mais provável algumas milhares de crianças nascerem no Brasil do que uma apenas (na verdade em 2022, cerca de 200 mil nascimentos ocorreram a cada mês de acordo com o noticias.uol.com.br).
Mas diminuiremos este intervalo para 1 dia. Acredito que seja razoável assumir que a chance de que mais de uma criança nascer ainda seja maior do que a de uma criança apenas nascer. Mas com certeza, a chance de 200 mil nascerem também é bem menor. E se o intervalo for de 1 minuto? Qual é a chance de que durante um minuto, dois bebês nasçam no Brasil? Essa chance é maior do que a de apenas um nascer?
Conforme olhamos para intervalos de tempo mais e mais curtos, eventos múltiplos ou até simultâneos se tornam cada vez mais raros.
Por causa disso, consideramos apenas as contribuições dos eventos únicos na dinâmica populacional, chamamos isso de aproximação de primeira ordem.
Voltemos nossa atenção para a pergunta: Qual é a probabilidade de que observemos a população com $N$ indivíduos após o intervalo de $t$ até $t + \Delta t$?
Como já sabemos os 4 possíveis eventos que os indivíduos em nossa população podem fazer, as possibilidades são
-
No momento $t$, o sistema já estava no estado $N$, e não mudou de estado durante o intervalo $\Delta t$;
-
No tempo $t$, o sistema estava com $N+1$ indivíduos e um indivíduo morreu por causas naturais, levando o sistema ao estado $N$;
-
Novamente, no tempo $t$ o sistema estava com $N+1$ indivíduos, porém um deles morreu devido à competição por recursos com seus vizinhos;
-
A população em $t$ era de $N-1$ indivíduos e um deles se reproduziu e gerou um novo integrante.
A probabilidade de transição para o item 2 é $ d (N+1) \Delta t \left( 1 - d N \Delta t \right)^N = d (N+1) \Delta t + \mathcal{O}(\Delta t^2)$. Onde aqui empacotamos todos os termos que possuem uma contribuição da potência de $\Delta t$ maior ou igual a 2 em como “termos de ordem $\mathcal{O}$ maior ou igual a $\Delta t^2$”. De forma análoga para o item 3, a probabilidade de ocorrência é $ \alpha (N+1) \Delta t + \mathcal{O}(\Delta t^2)$. Podemos representar a probabilidade total $P_{n+1 \rightarrow n} = (d + \alpha) (N + 1) \Delta t + \mathcal{O}(\Delta t^2)$.
Para o item 4, escrevemos diretamente $b(N-1) \Delta t + \mathcal{O}(\Delta t^2)$. E finalmente, o item 1 pode ser visto como 1 menos a probabilidade de 2, 3 e 4 ocorrerem, já que ao menos um dos 4 deve ocorrer.
Portanto, podemos escrever a probabilidade de observar o sistema com $N$ indivíduos, após um intervalo $\Delta t$ como
\[\begin{align} \nonumber P(N;t+\Delta t) & = \overbrace{P(N-1;t)}^{\text{prob. estar em N-1 no instante t}} \underbrace{b (N-1) \Delta t}_{\text{prob. reprodução}} + \\ \nonumber & + \overbrace{P(N+1;t)}^{\text{prob. estar em N+1 no instante t}} \underbrace{(d + \alpha)(N+1) \Delta t}_{\text{prob. morte}} + \\ \nonumber & + \overbrace{P(N;t)}^{\text{prob. estar em N no instante t}} \underbrace{(1 - bN\Delta t)(1 - dN \Delta t)(1 - \alpha N \Delta t)}_{\text{prob. nada acontece}} + \\ \nonumber & + \underbrace{\mathcal{O}(\Delta t^2)}_{\text{outros termos de ordem maior ou igual a } \Delta t^2} \end{align}\] \[\begin{align} \nonumber P(N;t+\Delta t) & = P(N;t)(1 - bN \Delta t - dN \Delta t - \alpha N \Delta t) + \\ \nonumber & + P(N-1;t)b(N-1) \Delta t +\\ \nonumber & + P(N+1;t)(d + \alpha)(N+1) \Delta t + \\ \nonumber & + \mathcal{O}(\Delta t^2) \end{align}\]E aqui parece que só deixamos as coisas mais confusas. A resposta para nossa pergunta parece depender da probabilidade de outros estados, que por sua vez tem suas próprias equações de probabilidade. A resposta parece longe e improvável, como se estivessemos adentro em um longo túnel escuro sem fim. Porém, como já dizia Tio Iroh em Avatar:
“Às vezes, a vida é como este túnel escuro, você não pode sempre ver a luz no final do túnel, mas se você continuar em movimento, você chegará a um lugar melhor.”
Nosso herói sem capa, cálculo, aparece agora. Porém, antes de invocá-lo, vamos tentar entender o que esta equação tenebrosa para a probabilidade $P(N;t + \Delta t)$ nos diz. A imagem a seguir esquematiza o que temos em nossas mãos:
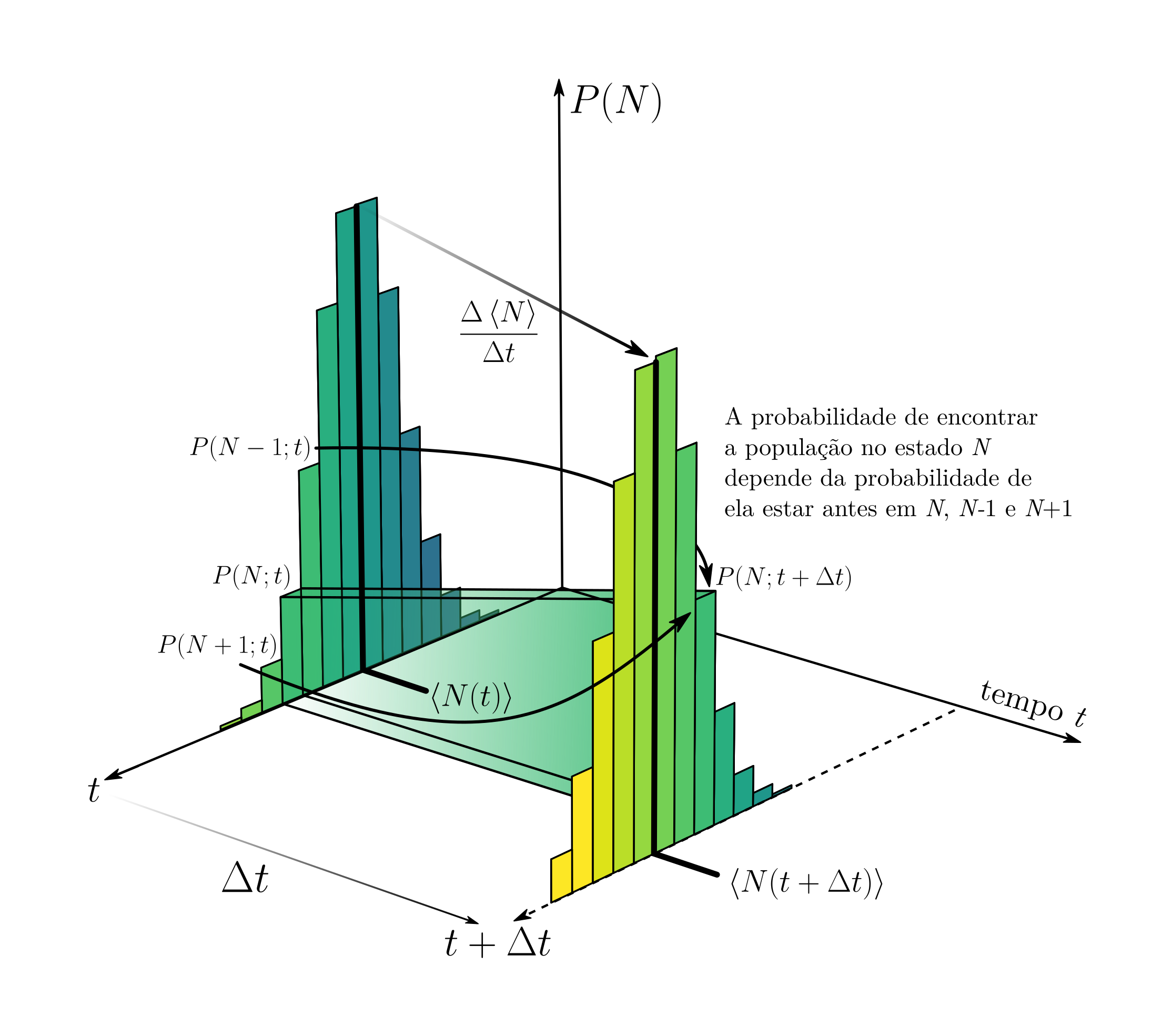
Nessa imagem, há 3 dimensões representadas. A vertical representa a probabilidade $P(N)$ de que a população esteja em um estado $N$. Barras mais altas vão indicar uma probabilidade maior. Os outros dois eixos que estão “no chão” indicam a dimensão do tempo, e o valor de $N$. No instante $t$, observamos que há vários valores de $N$ com probabilidade $P(N)$ maior que zero. Ao escolhermos um desses valores de $N$, calculamos o valor desta probabilidade em $t + \Delta t$ de acordo com a equação acima. Na imagem há duas setas indicando que $P(N+1;t)$ e $P(N-1;t)$ afetam o resultado de $P(N;t+\Delta t)$, como evidenciado na equação. Podemos pensar então que $P(N;t+\Delta t)$ depende das probabilidades de que a população esteja em $N+1$, $N-1$ e $N$ no instante $t$, cada probabilidade pesada pela chance de que reproduções ou mortes ocorrerem. Se quisessemos calcular como essa distribuição de probabilidade toda muda de um momento para outro, precisariamos calcular $P(N;t+\Delta t)$ para todos os valores de $N$.
Ao invés de se perguntar então sobre a chance de que a população esteja em um determinado nível, faz mais sentido se perguntar como essa chance muda conforme o tempo passa. Frequentemente na natureza é mais fácil explicar como as coisas mudam do que explicar porque elas estão do jeito que estão agora. Para isso, dividimos a probabilidade por $\Delta t$ e passamos o termo $P(N;t)$ para o lado esquerdo da equação, obtendo a taxa de variação da probabilidade conforme o tempo passa
\[\begin{align} \frac{P(N;t+\Delta t) - P(N;t)}{\Delta t} &= -P(N;t)(b+d+\alpha)n + P(N-1;t)b(N-1) \\ \nonumber & + P(N+1;t)(N+1)(d + \alpha) + \mathcal{O}(\Delta t), \end{align}\]e como mencionado anteriormente, tomamos o limite $\Delta t \rightarrow 0$.
\[\begin{align} \lim_{\Delta t \rightarrow 0} \frac{P(N;t+\Delta t) - P(N;t)}{\Delta t} = \frac{\mathrm{d}}{\mathrm{d}t}P(N;t), \end{align}\]finalmente obtendo
\[\begin{align} \boxed{ \frac{\mathrm{d}}{\mathrm{d}t}P(N;t) = -P(N;t)(b+d+\alpha)n + P(N-1;t)b(N-1) + P(N+1;t)(N+1)(d + \alpha) } \end{align}\]Aaahh vejam só, uma equação diferencial! Felizmente elas são muito mais tratáveis e como dizia Steven Strogatz:
“Desde Newton, a humanidade percebeu que as leis da natureza são sempre expressas na língua das equações diferenciais”
Na verdade está é justamente a equação mestra para este sistema!
Entretanto, essa equação é mais uma vez complicada demais, poís a probabilidade parar um estado $N$ depende da probabilidade de $N$, $N+1$ e $N-1$. E as probabilidades de $N+1$ e $N-1$ vão depender das probabilidades de $N+2$, $N$, $N-1$ e $N-2$, $N$ e $N-1$, respectivamente; e assim por diante. No fim teremos um sistema de sei la quantas centenas de ou milhares de equações diferenciais acopladas. Isso pode até ser solúvel para $N$ baixos, se estabelecermos um limite máximo para a distribuição de probabilidades de $N$, mas rapidamente se torna impraticável para $N$ altos.
E se então nos perguntarmos a respeito do comportamento médio ![]() ? E se ao invés de nos preocuparmos com a distribuição de probabilidades de $N$ em um dado instante $t$, nos perguntarmos qual é o valor médio de $N$ naquele instante? Aqui entra a nossa 5ª premissa, a de que nosso sistema é homogêneo o suficiente de forma que a média seja representativa da população inteira. Esse calculo do valor médio de $N$ é representado na imagem que mostrei a pouco, pelas linhas fortes que mostram o valor de $\left \langle N \right \rangle$ nos instantes $t$ e $t + \Delta t$. Ou seja, o que estamos fazendo aqui é assumindo que a variação temporal deste valor médio é descritivo da variação temporal da distribuição inteira. Para uma distribuição discreta, tal qual a distribuição de valores de população $N$, a média é calculada através de
? E se ao invés de nos preocuparmos com a distribuição de probabilidades de $N$ em um dado instante $t$, nos perguntarmos qual é o valor médio de $N$ naquele instante? Aqui entra a nossa 5ª premissa, a de que nosso sistema é homogêneo o suficiente de forma que a média seja representativa da população inteira. Esse calculo do valor médio de $N$ é representado na imagem que mostrei a pouco, pelas linhas fortes que mostram o valor de $\left \langle N \right \rangle$ nos instantes $t$ e $t + \Delta t$. Ou seja, o que estamos fazendo aqui é assumindo que a variação temporal deste valor médio é descritivo da variação temporal da distribuição inteira. Para uma distribuição discreta, tal qual a distribuição de valores de população $N$, a média é calculada através de
Aqui a notação $\left \langle N \right \rangle$ significa o valor médio de $N$. Leitores físicos provavelmente estão acostumados a esta notação e novamente peço desculpas aos amigos e amigas biológos pela possível confusão na mente de vocês com notações novas, mas pela minha formação acho a escrita dessa forma muito mais fluída e fácil.
Iremos tornar a equação mestra em uma equação diferencial para o valor médio de $N$. Multiplicando a equação mestra por $N$ e somando sobre todos os estados, obtemos
\[\begin{align} \frac{\mathrm{d}}{\mathrm{d}t} \left \langle N \right \rangle & = - (b + d+ \alpha) \sum_{N} N^2 P(N;t) + \\ \nonumber & + b \sum_{N} N^2 P(N-1;t) - \\ \nonumber & - b \sum_{N} N P(N-1;t) + \\ \nonumber & + (d + \alpha) \sum_{N} N^2 P(N+1;t) + \\ \nonumber & + (d+\alpha) \sum_{N} N P(N+1;t) \end{align}\]E agora parece que a situação piorou ainda mais. Antes tinhamos um sistema de equações acoplado e agora temos uma equação diferencial com vários somatórios??? Mas confiem no processo. Se pudermos deixar os somatórios no formato $\displaystyle \sum_{N} N P(N;t)$, poderemos escrever tudo apenas em termos das médias de $N$, já que essa soma é justamente a definição da média. O primeiro termo da equação diferencial já tem esse formato, e portanto nos atentaremos ao segundo. Se fizermos uma renomeação dos índices no somatório, passando de uma soma em $N$ para uma soma em um nov índice $M$, tal que $M = N - 1$, reescrevemos
\[\begin{align} b \sum_{N} N^2 P(N-1;t) = b \sum_{M} (M+1)^2 P(M;t) \end{align}\]Porém, $M$ é apenas um índice de soma e podemos nomeá-lo da forma como quisermos. Por isso iremos renomeá-lo novamente para $N$, de forma que
\[\begin{align} b \sum_{N} N^2 P(N-1;t) = b \sum_{N} (N+1)^2 P(N;t) \end{align}\]Isso pode parecer um truque sem sentido e talvez mágico para alguns, então permitam-me fazer um pause em nossa derivação afim de explicar o que ocorre aqui (quem não quiser ver pode continuar lendo após o —).
O que fizemos aqui na prática foi mover o somatório em 1 índice para trás. Isso pode soar um movimento ilegal e freestyle, mas peguemos um exemplo prático:
Suponha $P(0) = 0.05$, $P(1) = 0.15$, $P(2) = 0.3$, $P(3) = 0.3$, $P(4) = 0.15$, $P(5) = 0.05$ e $P(N>5) = 0$. Nesse caso
\[\begin{align} \nonumber & \sum_{N} N^2 P(N-1) = \\ & = \sum_{N=0}^\infty N^2 P(N-1) = 0\times P(-1) + 1^2 \times P(0) + \cdots + 6^2 \times P(5) + \cdots \end{align}\]naturalmente todos os termos que envolvem $P(6)$ em diante serão nulos, bem como o primeiro termo por envolver $P(-1) = 0$. O resultado desta soma é $13.7$. Poís bem, façamos uma mudança no índice de tal forma que $M$ agora é $N-1$. Neste caso
\[\begin{align} \nonumber & \sum_{N=0}^\infty N^2 P(N-1) = \\ & \sum_{M=-1}^\infty (M+1)^2 P(M) = 0^2\times P(-1) + 1^2 \times P(0) + \cdots + 6^2 \times P(5) + \cdots \end{align}\]Note que o somatório é o mesmo, inclusive o resultado continua sendo o mesmo $13.7$. Isso poís a relação entre os termos da soma ainda é a mesma, como você mesmo pode verificar escrevendo termo a termo da soma.
Expandindo o termo do somatório recém encontrado, podemos escrever
\[\begin{align} b \sum_{N} (N+1)^2 P(N;t) & = b \sum_{N} N^2 P(N;t) + 2 b \sum_{N} N P(N;t) + b \underbrace{\sum_{N} P(N;t)}_{=1} = \\ \nonumber & = b \sum_{N} N^2 P(N;t) + 2 b \sum_{N} N P(N;t) + b, \end{align}\]onde na última linha utilizamos a normalização $ \sum_{N} P(N;t) = 1$. O somatório no terceiro termo fica
\[\begin{align} b \sum_{N} N P(N-1;t) & = b \sum_{N} (N+1) P(N;t) = b \sum_{N} N P(N;t) + b \end{align}\]Analogamente para as somas envolvendo $P(N+1;t)$, fazemos a mudança de índice $M = N+1$ e obtemos, após a renomeação de $M$
\[\begin{align} (d + \alpha) \sum_{N} N^2 P(N+1;t) & = (d + \alpha) \sum_{N} (N-1)^2 P(N;t) = (d + \alpha) \sum_{N} N^2 P(N;t) - \\ \nonumber & - 2 (d + \alpha) \sum_{N} N P(N;t) + (d + \alpha) \end{align}\] \[\begin{align} \nonumber (d + \alpha) \sum_{N} N P(N+1;t) & = \\ (d + \alpha) \sum_{N} (N-1) P(N;t) & = (d + \alpha) \sum_{N} N P(N;t) - (d + \alpha) \end{align}\]Juntando tudo, a equação mestra fica escrita como
\[\begin{align} \frac{\mathrm{d}}{\mathrm{d}t} \left \langle N \right \rangle & = - (b + d+ \alpha) \sum_{N} N^2 P(N;t) + b \sum_{N} N^2 P(N;t) + 2 b \sum_{N} N P(N;t) + \\ \nonumber & + b - b \sum_{N} N P(N;t) - b + (d + \alpha) \sum_{N} N^2 P(N;t) - \\ \nonumber & - 2 (d + \alpha) \sum_{N} N P(N;t) + (d + \alpha) + (d + \alpha) \sum_{N} N P(N;t) - (d + \alpha) \end{align}\] \[\begin{align} \boxed{\frac{\mathrm{d}}{\mathrm{d}t} \left \langle N \right \rangle = b \sum_{N} N P(N;t) - d \sum_{N} N P(N;t) - \alpha \sum_{N} N P(N;t)} \end{align}\]Veja que caso $b$, $d$ e $\alpha$ sejam constantes, podemos escrever
\[\begin{align} \nonumber &\frac{\mathrm{d}}{\mathrm{d}t} \left \langle N \right \rangle = (b - d- \alpha) \sum_{N} N P(N;t)\\ & \frac{\mathrm{d}}{\mathrm{d}t} \left \langle N \right \rangle = \underbrace{(b - d- \alpha)}_{r} \left \langle N \right \rangle, \end{align}\]e essa equação se torna a mesma equação do crescimento exponencial, com a diferença que o termo de mortalidade é agora adicionado de um fator devido à competição por recursos, e ao invés de $b > d$ ser a condição necessária para o crescimento exponencial, precisamos ter $b > d + \alpha$. Ou seja, a taxa de reprodução da população precisa ser maior do que a soma da taxa de mortalidade por causas naturais com a taxa de mortalidade por competição intraespecífica.
Porém a taxa de mortalidade por competição de recursos é proporcional à probabilidade de que outro indivíduo adquira o recurso antes, levando o primeiro à fome. Naturalmente a chance de que isso ocorra é proporcional ao numero de indivíduos. Portanto em uma descrição mais realística a competição por recursos depende da quantidade de indivíduos na população. Quanto menos indivíduos, menor a necessidade de competir com vizinhos por comida, água, espaço, etc. Acontece que essa depêndencia pode assumir muitas formas, e muito provavelmente não ocorre de forma linear.Entretanto, pegando o espírito da aproximação de primeira ordem mencionado anteriormente, aproximamos a dependência da taxa de competição com a população por $\alpha = \alpha_0 N$. Isto é, a competição por recursos aumenta linearmente com o aumento da população. Apenas com essa melhoria, mantendo a taxa de mortalidade por causas naturais e a natalidade fixas, obtemos
\[\begin{align} \frac{\mathrm{d}}{\mathrm{d}t} \left \langle N \right \rangle & = b \sum_{N} N P(N;t) - d \sum_{N} N P(N;t) - \alpha_0 \sum_{N} N^2 P(N;t) = \\ \nonumber & = b \left \langle N \right \rangle - d \left \langle N \right \rangle - \alpha_0 \left \langle N^2 \right \rangle . \end{align}\]que parece ser a equação diferencial de um modelo logístico, porém note que está equação envolve a média de $N^2$, isto é, o segundo momento estatístico da distribuição de probabilidades para os estados possíveis do sistema. Precisamos ser capazes de encontrar $\left \langle N^2 \right \rangle$ para poder solucionar esta equação. Poderíamos refazer todo o processo para encontrar uma equação que descreva a variação temporal de $\left \langle N^2 \right \rangle$, e substituir a integral desta equação no último termo. Porém, está equação iria depender do terceiro momento estatístico $\left \langle N^3 \right \rangle$. Não ajudaria muito.
A aproximação de campo médio também supõe no fundo que todos os momentos estatísticos de ordem maior que 1 são dados em termos do primeiro momento estatístico (a média). Logo
\[\begin{align} \boxed{\frac{\mathrm{d}}{\mathrm{d}t} \left \langle N \right \rangle = b \left \langle N \right \rangle - d \left \langle N \right \rangle - \alpha_0 \left \langle N \right \rangle^2 = \left \langle N \right \rangle \left[ \underbrace{(b-d)}_{r} - \alpha_0 \left \langle N \right \rangle \right]} \end{align}\]Esta é a equação conhecida para um crescimento logístico!
No fundo, o que a aproximação de campo médio está dizendo nesta equação é que a variância na distribuição de probabilidade dos estados $N$, em um dado instante $t$, é nula. $\mathrm{Var}[N] = \left \langle N^2 \right \rangle - \left \langle N \right \rangle^2 = 0 \Rightarrow \left \langle N^2 \right \rangle = \left \langle N \right \rangle^2$. Caso a variância não seja nula, podemos reescrever a equação como
\[\begin{align} \frac{\mathrm{d}}{\mathrm{d}t} \left \langle N \right \rangle = b \left \langle N \right \rangle - d \left \langle N \right \rangle - \alpha_0 \left( \left \langle N^2 \right \rangle + \mathrm{Var}[N] \right) \end{align}\]Ou seja, a presença de uma variação na distribuição de probabilidade de estados do sistema, naturalmente provoca uma diminuição no valor esperado de $N$ para um dado instante de tempo $t$. A estocasticidade não apenas provoca flutuações em torno da média, como também é capaz de mudar o próprio valor esperado de população $t$ tempo após o início da dinâmica.
E agora que chegamos ao fim dessa derivação, e encontramos a tão famosa equação diferencial do modelo logístico, vamos parar para ver algumas coisas:
A primeira delas é que tivemos que assumir 5 premissas para chegar nela:
- Os indivíduos só interagem com sua comida e entre si.
- A reprodução ocorre de forma assexuada.
- Todos os indivíduos são iguais e possuem a mesma aptidão.
- Eventos de morte, reprodução ou competição que ocorrem com um indivíduo, não dependem do que ocorre com os outros indivíduos.
- O sistema é espacialmente homogêneo.
Somado a isso há a suposição de que a variância na distribuição de probabilidade de estados de $N$ é nula. E que a taxa de competição é linearmente dependente da população $\alpha = \alpha_0 N$.
Muita coisa teve que ser suposta como verdade para chegarmos nessa equação. Em laboratório, é muito mais fácil atingir estes requerimentos, o que torna a verificação dessa equação muito mais papável. Isso não torna a equação inútil na vida real fora do laboratório, ela serve como a base para descrever o comportamento das populações em nível mais básico. Podemos por exemplo, dividir a população em machos $M$ e fêmeas $F$ e assumir uma reprodução sexuada, eliminando uma das premissas. Cada uma delas pode ser atacada individualmente para aproximar o modelo da realidade.
Mas para que serve um modelo?
Seu único e exclusivo fim é descrever a realidade com a melhor exatidão possível? Ou ele serve como uma ferramenta para entender o papel de diversos mecanismos que atuam em um sistema? Se a sua resposta tender ao primeiro caso, então receio que nenhum modelo (seja matemático ou não) irá lhe satisfazer. Já no segundo caso, começamos a ver o papel do modelo logístico, ao observarmos um sistema que obedece de forma razoável o comportamento descrito pelo modelo logístico, podemos dizer que as 5 premissas são satisfeitas? Não, mas podemos afirmar que os outros mecanismos que sem dúvida estão presentes talvez não sejam dominantes na vida dos indivíduos que compõe esta população.
Como um exemplo, trarei o leitor para a minha área de formação, a física. Quando aprendemos física no ensino médio, sempre desprezamos a resistência do ar. Porque? Porque passar 3 anos aprendendo fórmulas e leis que não descrevem aquilo que encontramos todos os dias? Há dois motivos para isso, no meu ver. O primeiro está relacionado à dificuldade, é muito mais fácil começar pelo mais simples (e já vemos o trauma que isso causa em muitos alunos). Incluir a resistência do ar em, digamos, o lançamento parabólico de objetos, envolve resolver uma equação diferencial de 2ª ordem
\[\begin{align} \frac{\mathrm{d}\vec{v}}{\mathrm{d}t} = -\vec{g} - \frac{1}{2} \rho C_d A \vec{v}^2, \end{align}\]na qual eu acho razoável argumentar que alunos de ensino médio não possuem a maturidade para compreender e interpretar. O segundo motivo está relacionado aos mecanismos. Sim, claro que o ar está sempre presente, mas não é ele que determina majoritariamente a trajetória de uma bolinha atirada no ar na maioria das vezes. Quem determina isso é a força gravitacional. A resistência do ar ocupa um papel muito pequeno nestes casos, de forma que ensinar os alunos equações e fórmulas que envolvam-na se torna mais uma distração do que é realmente mais importante e mais geral do que uma adição valiosa para o saber do aluno sobre o funcionamento do mundo.
O modelo logístico faz esse mesmo papel na ecologia. Ele é a 2ª lei de Newton para a ecologia, ele é o caso ecológico da mecânica sem resistência do ar, rotação, carga elétrica e tudo mais. Mas é através dele que notamos alguns comportamentos gerais.
E por fim, no caso da resistência do ar, a descrição é tão boa sem ela, que muitas vezes nem precisamos considerá-la. Em cenários ecológicos o mesmo ocorre, algumas interações entre indivíduos podem estar sempre presentes, mas dependendo da escala de tempo e precisão que nos interessa, elas se tornam desprezíveis.