Teoria da informação e Wordle

Você talvez já tenha visto ou jogado o jogo wordle, ou o termo (a versão pt-br do wordle). É um jogo onde todos os dias uma palavra secreta é escolhida, e o objetivo é adivinhar a palavra em no máximo 6 tentativas, com base em algumas dicas. Você começa chutando uma palavra qualquer (só podem ser palavras de 5 letras) e o jogo te diz se as letras da palavra que você chutou existem na palavra secreta, se não existem, e se estão na mesma posição que você colocou.

Por exemplo, se a palavra é beijo e seu primeiro chute é jeito, o jogo irá de dizer que o j está na palavra secreta, porém em outra posição; o e está na palavra secreta e está na posição correta; o i também, o t não está na palavra secreta; e o o está e também está na posição correta, assim como o ei. O jogo diz isso colorindo a posição de cada palavra para você, tipo assim:

Tentativa: jeito
Feedback:

Com essa informação, você chuta uma nova palavra. Tente jogar uma partida aqui: termo.pt

Acontece que no primeiro chute, você não tem nenhuma informação sobre a palavra secreta, então vem a pergunta: Existe uma palavra que é um chute inicial melhor do que outras?

A princípio pode parecer que não, a resposta pode ser qualquer palavra e a chance de que você acerte no primeiro chute é ínfima. De acordo com o repositório de palavras da língua portuguesa do IME-USP, há 5481 palavras com cinco letras na língua portuguesa brasileira, excluindo nomes de cidades. Portanto existe 1 em 5481 chances de você acertar a palavra de primeira, supondo que todas as 5841 palavras estejam inclusas como possíveis respostas para o jogo.

Mas o nosso objetivo no primeiro chute não deve ser acertar de primeira, mas sim escolher a palavra que nos de as informações mais uteis para pensarmos em qual deve ser a palavra secreta. Por exemplo, sabemos que muitas palavras do português possuem a letra a e e, enquanto pouquíssimas possuem a letra x. Saber quais letras estão inclusas ou não, é uma informação valiosa. Então voltamos à pergunta: Existe uma palavra que é um chute inicial melhor do que outras? Ou melhor ainda, existe uma palavra que nos dê mais informação do que outras?

O meu objetivo aqui nesse texto é mostrar que sim, e encontrar qual é a melhor palavra para servir de chute inicial no termo usando teoria da informação. Antes vale dizer que estas anotações são praticamente uma tradução do vídeo Solving Wordle using information theory, do canal 3Blue1Brown. Se você é confortável com inglês, acredito que valha mais a pena assistir ao vídeo do que ler esse texto, aqui estarei basicamente aplicando o que é mostrado no vídeo para o termo ao invés do wordle, ou seja, usando português ao invés de inglês.

O melhor chute inicial

Se você já jogou termo na época em que ele foi uma febre, você provavelmente tinha uma palavra favorita que gostava de usar nas primeiras tentativas.

Para quantificarmos qual o melhor chute inicial, vamos supor que inicamos com a palavra beijo. Não sabemos qual é a palavra secreta, e portanto não sabemos qual será o feedback que o jogo nos dará. Se o feedback for por exemplo:

Sabemos que as letras e e i estão na resposta final, porém em posições diferentes, enquanto que as demais não estão. Essa informação nos permite eliminar muitas palavras, como “bomba”, já que sabemos que b não está contido na resposta. Na verdade, sobram 293, das 5481 palavras. E se o feedback do jogo fosse outro? Por exemplo:

Nesse caso restariam 142 palavras. Podemos fazer isso com todos os possíveis feedbacks que o jogo nos dá. Temos 3 opções de feedback para cada uma das 5 letras da palavra, portanto o total de feedbacks possíveis é $N = 3 \times 3 \times 3 \times 3 \times 3 = 3^5 = 243$. Em cada um deles, vai existir uma quantidade $n$ de palavras restantes que atendem às informações fornecidas pelo jogo. Como não sabemos qual é a palavra secreta, cada feedback tem uma chance $p$ de ocorrer dado pela quantidade de palavras restantes dividido pelo total de palavras de 5 letras inicialmente. Ou seja

\[\begin{align} p = \frac{n}{5481} = \frac{n}{M} \end{align}\]

Aqui, $M$ representa o total de palavras possíveis na língua portuguesa (ou em qualquer outra língua na qual o jogo seja feito). No caso de beijo como chute inicial, podemos organizar cada possibilidade de feedback do mais provável para o menos provável, usando todas as $M$ palavras possíveis de resposta.

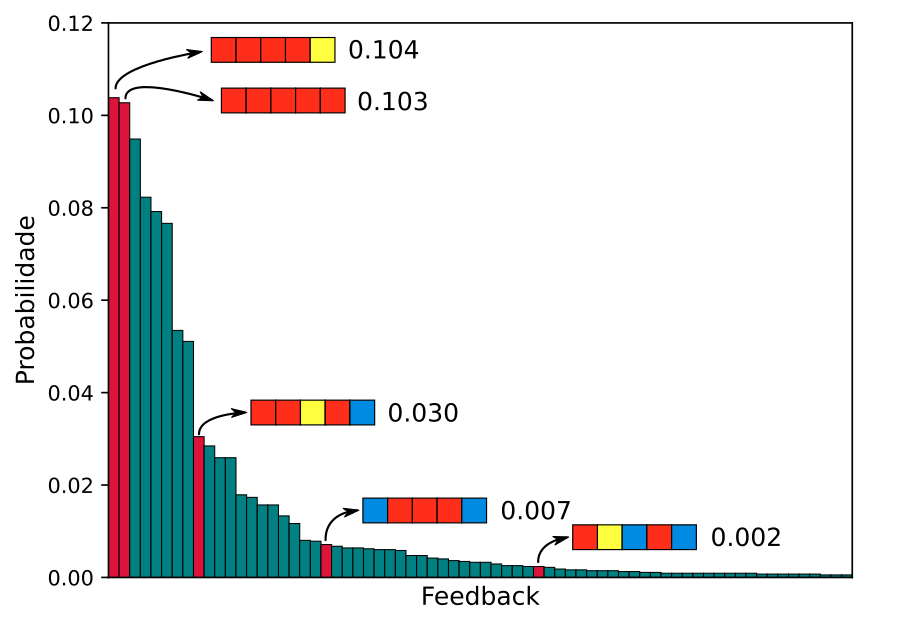
Para 10.4% das possíveis respostas, obtemos um feedback de beijo que nos diz que todas as letras não estão na resposta, exceto o o no final, que está na resposta, mas em outra posição. O segundo feedback mais comum (10.3%) é o que nos diz que erramos todas as letras. Notem que os mais provaveis são justamente aqueles onde a maior parte das letras na palavra estão incorretas. O que faz sentido, há muitas palavras no português que não possuem nenhuma dassas letras, ou apenas algumas delas, em posições diferentes. Mas como saber se esse é um bom chute? É claro que há mais chances de que no final tenhamos um feedback do jogo que não nos da tanta informação assim, mas também podemos ter um feedback que nos diz muita coisa! Faz sentido então pensarmos em o que é esperado desse chute. Em outras palavras, qual é o nível médio de informação que este chute nos dá?

E aqui pode parecer algo esquisito tentar medir informação de um chute de palavra, o que é uma sensação totalmente razoável, no nosso dia a dia nos referimos a informação como sendo algo um tanto subjetivo e não mensurável objetivamente. Entretanto, neste caso, informação é uma grandeza bem mensurável e clara. Entramos aqui no reino da teoria da informação .

A informação que obtemos ao se fazer uma escolha, está associada à o quão incerto ainda estamos a respeito da resposta correta. Um chute que nos deixe muitas opções restantes para a resposta não nos fornece muita informação. Pensem como uma loteria, saber que 2 sequências específicas de números não vão ganhar a loteria não nos ajuda muito, pois ainda existem milhares de opções ocultas e qualquer uma delas pode ser a ganhadora. Agora saber que uma das 2 sequências específicas vai ganhar a loteria é uma informação extremamente valiosa. Portanto, quanto mais raro um evento, mais informação ele tem para nós. Sendo assim, chegamos na primeira característica da nossa medida de informação:

1. A quantidade de informação obtida em nossa medida (por medida, entendam um chute, apenas estou introduzindo a terminologia mais usual da área) diminui conforme a probabilidade do resultado da medida aumenta.

Ainda na mesma linha de pensamento, se um resultado tem 100% de chance de ocorrer, ele não nos adiciona nenhuma informação nova. Por exemplo, suponhamos um chute com letras que não existem no português “æe̯ßßɛ”. Não existe nenhuma palavra no português com essas letras e naturalmente só há uma opção de feedback para esse chute, que é . Esse chute também não diminui em nada o nosso vasto espaço de opções para a resposta, portanto ele não nos traz nenhuma informação. Como consequência, a segunda característica da nossa medida de informação é

1. Quando a probabilidade de um resultado é 100%, a informação que ele nos dá é 0.

Por último, dois chutes consecutivos nos trazem informação nova que é adicionada à informação anterior. Ou seja, se temos o resultado $A$ e depois o resultado $B$, a quantidade total de informação que temos é $I(A) + I(B)$, onde $I$ é a quantidade de informação. Chegamos então à última característica de nossa medida de informação:

1. A informação de dois eventos consecutivos é somada. $I(AB) = I(A) + I(B)$.

Felizmente, essas três características são o suficiente para descrevermos matematicamente como a probabilidade de um resultado nos fornece mais ou menos informação.

Comecemos pela característica 3

\[\begin{align} I(AB) = I(A) + I(B) \end{align}\]

Suponhamos que essa função $I$ é contínua e pode ser derivada. Se derivarmos está equação com relação à $A$, obtemos o resultado

\[\begin{align} B \frac{\mathrm{d}}{\mathrm{d}A}I(AB) = \frac{\mathrm{d}}{\mathrm{d}A} I(A) \end{align}\]

E isso parece não ter ajudado absolutamente nada. Mas seguiremos agora derivando em relação a $B$

\[\begin{align} \frac{\mathrm{d}}{\mathrm{d}A}I(AB) + AB \frac{\mathrm{d^2}}{\mathrm{d}B \mathrm{d}A}I(AB) = 0 \end{align}\]

Mas $A$ e $B$ são só dois eventos quaisquer, e a combinação deles pode ser considerada um evento único. Portanto introduzimos agora a mudança de variáveis $AB = p$. Ou seja, podemos reescrever

\[\begin{align} \frac{\mathrm{d}}{\mathrm{d}p}I(p) + p \frac{\mathrm{d^2}}{\mathrm{d}p^2}I(p) = 0 \end{align}\]

Chegamos em uma equação diferencial para a função $I(p)$. Como resolver isso? Notem que (se não notarem tudo bem, eu só notei depois de olhar a resposta na internet) essa equação diferencial parece com uma regra do produto para a derivada de $p I’(p)$, onde o $I’$ indica derivada de $I$. Ou seja, essa equação diferencial pode ser escrita como

\[\begin{align} \frac{\mathrm{d}}{\mathrm{d}p}\left[ p \frac{\mathrm{d}}{\mathrm{d}p}I(p) \right] = 0 \end{align}\]

E por integração direta, chegamos em

\[\begin{align} p \frac{\mathrm{d}}{\mathrm{d}p}I(p) = k \end{align}\]

O resultado dessa equação diferencial de primeira ordem é

\[I(p) = k \log(p) + c\]

Porém, de acordo com a 2ª característica que tinhamos, $c = 0$ para que $I(1) = 0$. Ainda mais, de acordo com a 1ª característica, $k < 0$, para que aumentando a probabilidade $p$ de um resultado, a informação diminua. Só que escolher um valor de $k$ é análogo a escolher uma base $b$ arbitrária para o log, portanto podemos ignorar o valor exato de $k$ e representar o resultado como

\[I(p) = \log_b \left( \frac{1}{p} \right)\]

Nesse caso, $b$ determina a unidade de medida da nossa quantidade de informação $I$. Escolheremos $b=2$ para representar a informação de um chute em bits.

E qual é a interpretação do bit? Um bit representa a quantidade de informação que temos ao obter um resultado com probabilidade de 50%. Ou seja, se um chute de palavra diminui o espaço de possibilidades pela metade, esse chute possui 1 bit de informação. Mas, como vimos mais cedo, há muitas possibilidades de resultado para um dado chute, algumas mais prováveis que outras. Então para ranquear nossos chutes, estaremos nos atentando à quantidade de informação média do chute, ou seja, somamos todas as possibilidades de resultados e a informação obtida em cada uma delas, multiplicada pela probabilidade de obtermos esse resultado.

\[H = \sum_{i=1}^N p_i \log_2 \left( \frac{1}{p_i} \right)\]

Essa medida $H$ é chamada de entropia. O nome pode parecer uma surpresa para muitos, afinal de contas, essa medida de informação média de uma medida (no nosso caso, chute) não parece ter absolutamente nada a ver com a entropia termodinâmica que sempre ouvimos falar. Mas acreditem que tem, só não é o intuito desse texto falar disso.

Lembre-se que por definição, a informação de chutes consecutivos é adicionada, portanto se o primeiro chute nos da 2 bits de informação e o segundo mais 3 bits, temos um total de 5 bits de informação a respeito da resposta. Isso significa que conseguimos diminuir o espaço de possíveis palavras em 32x. Ou seja, quanto mais informação for esperada para um chute, melhor ele. Isso significa que podemos usar essa ideia não apenas para saber qual é o melhor chute inicial, mas também para saber quais são os melhores chutes a cada instante do jogo, sempre mantendo em mente o espaço de possibilidades restante.

Vamos voltar agora para o nosso chute inicial: beijo. Vimos já qual é a distribuição de possíveis feedbacks para este chute, agora vamos nos perguntar, qual é a quantidade média de informação que este chute nos dá? Fazendo esta soma, a quantidade média de informação que obtemos para o chute beijo é 4.72 bits. Em outras palavras, este chute possui uma entropia de 4.72 bits. Em média, a quantidade de informação que conseguimos com o chute beijo é equivalente a diminuir o espaço de possíveis respostas em aproximadamente 26x. Em comparação, um chute inicial como marca possui uma entropia de 5.03 bits. Um pouco maior.

Voltemos então à pergunta inicial, qual é o melhor chute inicial? Bem, se estivermos buscando a palavra que nos dê, em média, mais informação a respeito da palavra secreta, o melhor chute inicial é seria, nos fornecendo, em média, 6.34 bits de informação. Abaixo, eu vou colocar a lista de quais são as 5 melhores palavras de chute inicial e a quantidade de informação em bits que cada uma delas nos da:

palavra	informação (bits)
seria	6.34
serão	6.33
roías	6.31
raies	6.26
sério	6.26

Raies foi o mais inesperado para mim, eu nunca ouvi essa palavra antes, mas aparentemente ela vem do verbo “raiar” e é sinônimo de “alvoreças” ou “amanheças”.

Pausemos agora para pensar um pouco em o que a entropia está nos dizendo a respeito da distribuição de possíveis feedbacks para cada chute. Uma vez que a soma de todas as possibildiades tem que ser 100%, afinal de contas, a resposta precisa estar em alguma das possíveis palavras, temos que

\[\sum_{i}^N p_i = 1\]

Isso quer dizer que, se a probabilidade de um feedback $i$ for alta, as dos demais precisa ser baixa, o que aumenta a quantidade de informação em cada um deles, porém, os torna menos prováveis de ocorrer. A entropia será máxima no caso em que a probabilidade de cada resultado for igual. Ou seja, a entropia será máxima no caso em que a distribuição de possíveis feedbacks for uniforme, e cada um deles tiver chances iguais de ocorrer. No nosso caso, temos $3^5 = 243$ possíveis feedbacks, ou seja

\[\begin{align} \nonumber H &= \sum_{i}^N \frac{1}{N} \log_2 \left( \frac{1}{1/N} \right) = \sum_{i}^N \frac{1}{N} \log_2(N) = \\ & = N \left( \frac{1}{N} \log_2(N) \right) = \log_2(N) = \log_2(3^5) = \\ \nonumber & = 7.92 \text{ bits}. \end{align}\]

Este é o máximo de informação que poderíamos conseguir, em média, com um chute neste cenário. Infelizmente, não existe palavra no português que faça com que a distribuição de possíveis feedbacks seja uniforme. Portanto, podemos comparar o valor de entropia de um chute com o que seria esperado para uma distribuição uniforme que contenha a mesma entropia. O que isso quer dizer?

Suponhamos um chute que cuja entropia seja de 4 bits de informação. Isso é a mesma entropia que uma distribuição uniforme de 16 possíveis valores ($N = 16$). Se pegarmos agora um chute cuja entropia seja 6 bits, ele é equivalente à entropia de uma distribuição uniforme de 64 possíveis valores. De certa forma então, a entropia nos diz que, dada distribuição de probabilidade para um resultado que possua entropia $H$, ela tem o mesmo nível de incerteza que um cenário com probabilidades iguais de qualquer um de $2^H$ resultados. No caso dos chutes, se nosso chute tiver uma entropia de 6 bits, sabemos que há tanta incerteza nas possibilidades de feedback, que haveria caso tivessemos 64 possíveis feedbacks, todos igualmente prováveis.

Isso significa que a entropia de um dado chute também nos diz o quanto de incerteza esperamos diminuir com este chute, o que é basicamente outra forma de quantificar a informação que ganhamos em cada chute.

Claro que, em todo este texto eu assumi que a probabilidade de uma palavra ser a palavra secreta é uniforme, ou seja, todas as $M$ palavras de 5 letras no português tem a mesma probabilidade $1/M$ de serem a resposta. As coisas mudam se palavras mais usadas frequentemente tiverem maior chance de serem a resposta. Por exemplo, intuitivamente podemos imaginar que beijo tem muito mais chance de ser a resposta do que raies, uma vez que essa é uma palavra muito mais comumente usada. Ainda assim, é impressionante que podemos quantificar informação e relacionar ela com o que é estar incerto a respeito das possibilidades de um resultado!