Pedro Cintra

🦆 Meu site pessoal

Nota: Boa parte das contas apresentadas aqui neste texto são baseadas no artigo encontrado na referência 1.

Descrição do sistema

Considere uma rede de sítios que podem estar ocupados ou vazios por um indivíduo. Cada sítio pode representar um pequeno pedaço de espaço físico onde indivíduos podem habitar e explorar, ou pode ser uma representação mais abstrata para quantificar onde indivíduos podem estar. No primeiro caso, a descrição deste sistema se assemelha muito à descrição de redes de átomos em física da matéria condensada, onde partículas em uma rede cristalina ocupam sítios e cada sítio pode ser caracterizado pelo spin da partícula que o ocupa.

Neste sistema, sítios podem possuir dois estados possíveis:

(de forma análoga, em um sistema de uma rede de spins podemos dizer que um sítio pode possuir os estados spin up ou spin down)

A característica que difere este sistema ecológico de um sistema físico está na forma como descrevemos a interação entre sítios. Para os leitores físicos interessados, podem notar que esta descrição de um sistema se assemelha muito a um modelo de Ising.

Reações:

Em um sistema físico de spin, a interação entre sítios é descrita, usualmente, como uma interação entre sítios vizinhos na rede que exercem influência um no outro através da interação magnética entre o spin das partículas em cada sítio. Em nosso cenário ecológico, a dinâmica de um dado sítio será dada de forma simplificada por três possíveis reações:

  1. Nascimento (0 $\rightarrow$ 1): Sítios ocupados produzem novos indivíduos com uma taxa $b$, que são enviados aleatoriamente para um dos $z$ sítios vizinhos ao sítio focal, independente do estado da vizinhança $\mathcal{N}(i)$
  2. Morte natural (1 $\rightarrow$ 0): Sítios ocupados morrem de forma natural, independente do estado da rede, com uma taxa $\gamma$
  3. Morte por aglomeração (1 $\rightarrow$ 0): Sítios ocupados morrem devido à aglomeração (que leva à competição por recursos) com uma taxa $1 + \delta \times$(n° de vizinhos ocupados)

A figura abaixo representa o sistema em rede descrito por este modelo. O sítio focal $i$ possui uma vizinhança de interação $\mathcal{N}(i)$ composta por $z$ sítios, nos quais alguns estão ocupados (círculos coloridos preenchidos) ou vazios (círculos tracejados brancos). Os demais sítios nesta rede que não são coloridos não fazem parte da vizinhança de $i$.

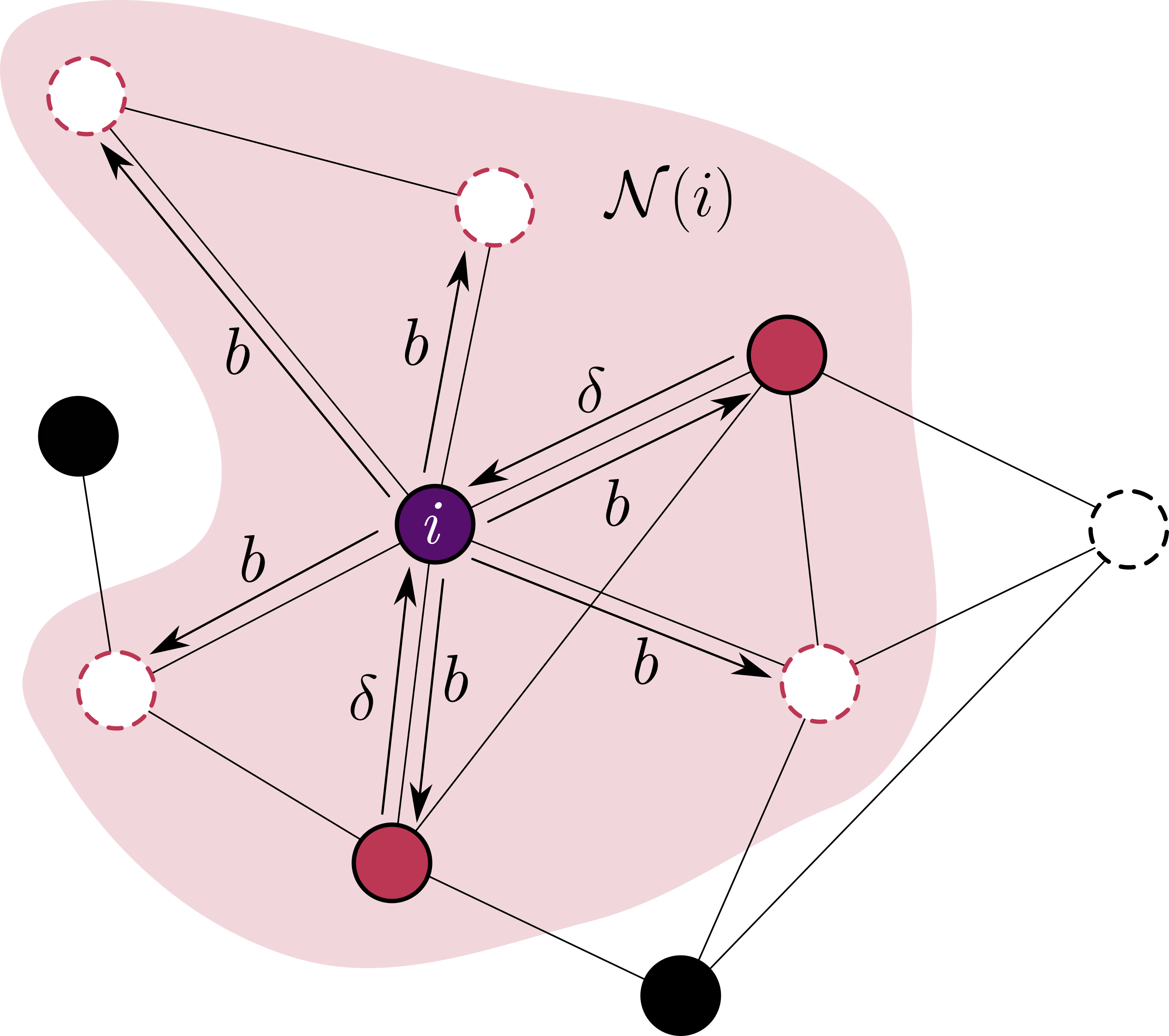
Neighborhood

Nesta ilustração, $i$ é influenciado pelos dois vizinhos ocupados, causando a aglomeração. Ao mesmo tempo, $i$ influencia todos os seus vizinhos através da reprodução e nascimento de um novo indivíduo. Além disso, $i$ influencia a si mesmo podendo causar sua morte natural (velhice, doença não infecciosa, azar…). A natureza da influência vinda da aglomeração é dada por relações ecológicas, que podem ser benéficas ou maléficas. Em nosso cenário, estamos considerando a competição por recursos, portanto um elevado número de vizinhos próximos competindo por recursos em comum leva à uma maior chance de morte por fome.

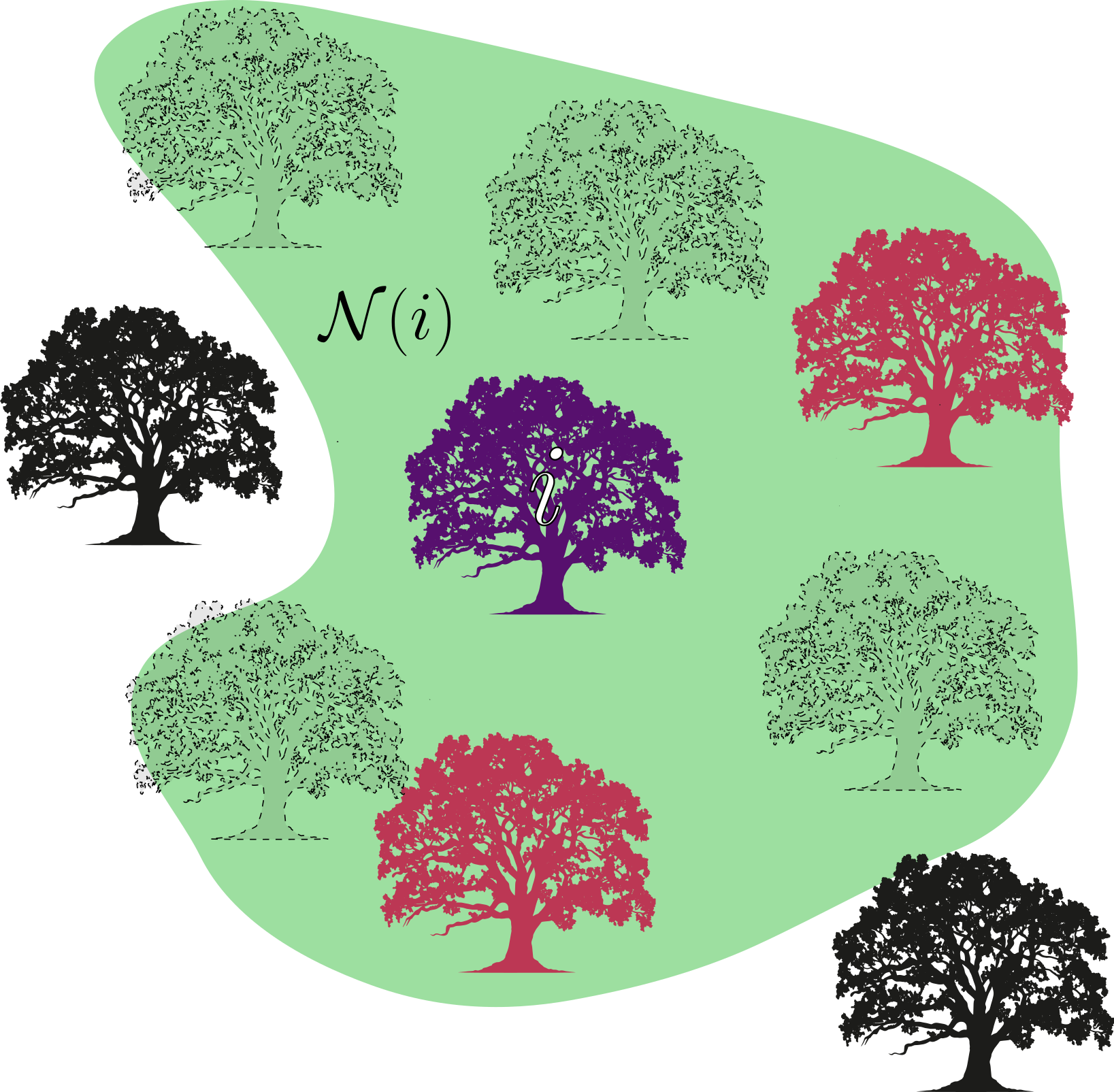
Como uma ilustração mais visual, considere um pequeno pedaço de vegetação onde um grupo de árvores cresce. Novamente, o indivíduo focal $i$ compete com as demais árvores ao redor de sua região por acesso à alimento e espaço para as raízes. Na imagem abaixo, árvores tracejadas representam locais vazios na região $\mathcal{N}(i)$ que define a vizinhança de $i$. Assumimos que uma árvore descendente de $i$ não é dispersada para longe da região de interação de $i$. Podemos generalizar o resultado que será mostrado a seguir para casos onde a vizinhança de competição $\mathcal{N}_c(i)$ e a vizinhança de reprodução $\mathcal{N}_r(i)$ são diferentes, abrangendo casos onde a dispersão é de longa distância (através de polinizadores, por exemplo). Mais tarde, incluiremos também a movimentação de indivíduos pelo espaço, de forma que nosso exemplo se torna mais generalizável a animais herbívoros que vivem sem grandes riscos de predação, como populações de bufalos africanos no Serengeti [2] e megaherbívoros, que excedem 1000 kg em peso quando adultos, no Parque Nacional Kruger [3].

Neighborhood

Pair Approximation - Modelo Logístico - $\mathcal{N}_c(i) = \mathcal{N}_r(i)$

Consideremos primeiro o caso onde a vizinhança de dispersão para reprodução e a vizinhança de competição são iguais.

Equação Mestra

Seja $P(\vec{n}, t)$ a probabilidade de que a rede tenha a configuração $\vec{n} = (n_1, n_2, \ldots, n_N)$ no instante $t$, onde $n_i \in {0,1}$ é o estado do sítio $i$, a equação mestra para a mudança da probabilidade no tempo é dada por (eu fiz uma pequena derivação de como chegar na equação mestra específica para um modelo logístico aqui, mas aqui abaixo eu deixo a formulação mais geral):

\[\frac{dP(\vec{n}, t)}{dt} = \sum_{\vec{n}'} [W(\vec{n}|\vec{n}') P(\vec{n}', t) - W(\vec{n}'|\vec{n}) P(\vec{n}, t)]\]

onde $W(\vec{n}’|\vec{n})$ e $W(\vec{n}|\vec{n}’)$ são as taxas de transição dos estados $\vec{n}$ para $\vec{n}’$ e vice-versa. A soma em $\vec{n}’$ é feita sobre todas as possíveis configurações de $\vec{n}’$. Trabalhemos agora nestas taxas de transição.

Taxas de transição $W(\vec{n}’|\vec{n})$:

Sendo $\mathcal{N}(i)$ é a vizinhança do sítio $i$ e $\hat{e}_i$ é o vetor unitário do sítio $i$, $\hat{e}_i = (0,0,\cdots,1,\cdots,0)$.

  1. Nascimento ($0 \to 1$ no sítio $i$): A taxa com a qual um sítio $i$ que está no estado $0$ muda para o estado $1$, através do nascimento de um novo indivíduo depende da quantidade de vizinhos ocupados na vizinhança de $i$, cada vizinho ocupado tem chance de enviar um novo indivíduo para o sítio $i$ com probabilidade $1/z$. Portanto:

    \[W(\vec{n} - \hat{e}_i|\vec{n}) = b \sum_{j \in \mathcal{N}(i)} n_j \cdot \frac{1}{z} \quad \text{se } n_i = 0\]

  2. Aglomeração ($1 \to 0$ no sítio $i$): A taxa de morte por aglomeração, que faz um sítio transitar de $1$ para $0$, depende do estado do sítio focal $i$, e a quantidade de vizinhos ocupados, cada um deles contribuindo com $\delta$ na taxa total de morte por aglomeração.

    \[W(\vec{n} + \hat{e}_i|\vec{n}) = \left( \delta \sum_{j \in \mathcal{N}(i)} n_j\right) n_i\]

  3. Morte natural ($1 \to 0$ no sítio $i$) Já a transição de $1$ para $0$ por morte natural depende apenas do próprio estado do sítio focal $i$, e a taxa de ocorrência desta reação:

    \[W(\vec{n} + \hat{e}_i|\vec{n}) = \gamma n_i\]

Equações para médias

Com essas taxas de transição, podemos montar a equação mestra para o sistema. Entretanto, a equação mestra é muito frequentemente intratável do ponto de vista analítico e até computacional. Por isso, simplificamos nosso interesse aqui. Ao invés de querermos descrever toda a distribuição de probabilidade $P(\vec{n},t)$, estaremos interessados na média desta distribuição. Em outras palavras, iremos focar nosso esforços em descrever o comportamento médio, a partir do valor esperado de $n$. Tomando o valor esperado, definimos as seguinte densidades:

A partir da equação mestra:

\[\frac{d\rho_1}{dt} = \left \langle \frac{dn_i}{dt} \right \rangle = \sum_{\vec{n}} n \frac{d P(\vec{n},t)}{dt}\]

Isso nos resultará algumas algebras de manipulação de índices em somatórios, que eu já fiz com mais detalhes aqui. Feitas estas manipulações, podemos calcular as contribuições de cada reação para a média de ocupação da rede, em termos das densidades previamente definidas.

Contribuição do nascimento:

\[\frac{b}{z} \sum_{j \in \mathcal{N}(i)} \langle n_j (1 - n_i) \rangle = \frac{b}{z} \cdot z \cdot \rho_{10}\]

Usando a probabilidade condicional: \(P(\text{vizinho ocupado | sítio i está vazio}) = q_{1|0} = \frac{\rho_{10}}{\rho_0} \Rightarrow\) \(\Rightarrow \rho_{10} = q_{1|0} \rho_0\)

Portanto a taxa de nascimento fica: $b q_{1|0} \rho_0 = b q_{1|0} (1-\rho_1)$

Contribuição da aglomeração:

\[-\left \langle \left(\delta \sum_{j \in \mathcal{N}(i)} n_j\right) n_i \right \rangle = -\delta z q_{1|1}\rho_1\]

Contribuição da morte natural:

\[-\gamma \langle n_i \rangle = -\gamma \rho_1\]

portanto:

\[\boxed{\frac{d\rho_1}{dt} = bq_{1|0}(1-\rho_1) - (\delta z q_{1|1} + \gamma)\rho_1}\]

Esta equação é exata! Isso significa que ela é a descrição mais precisa do comportamento médio da distribuição de probabilidade $P(\vec{n},t)$. Entretanto, ela depende de $\rho_{11}$, poís $q_{1|1} = \rho_{11}/\rho_{1}$. Para conseguirmos resolver o sistema sem invocar a aproximação de campo médio, precisamos de uma equação para a frequência de pares $\rho_{11}$. Caso quiséssemos trabalhar com a aproximação de campo médio, teríamos $\rho_{11} = \rho_{1}^2$, como consequência da suposição de que as interações entre vizinhos são homogêneas.

Derivação da equação do par $\rho_{11}$

Para a densidade de pares $\rho_{11}$:

\[\frac{1}{2}\frac{d\rho_{11}}{dt} = \left \langle \frac{d(n_i n_j)}{dt} \right \rangle \text{ para vizinhos } i,j\]

Contribuição do nascimento:

Cada sítio ocupado produz filhotes a uma taxa $b$, enviado-os para um dos $z$ vizinhos com igual probabilidade $1/z$.

Para que um par $(1,1)$ seja criado a partir do nascimento:

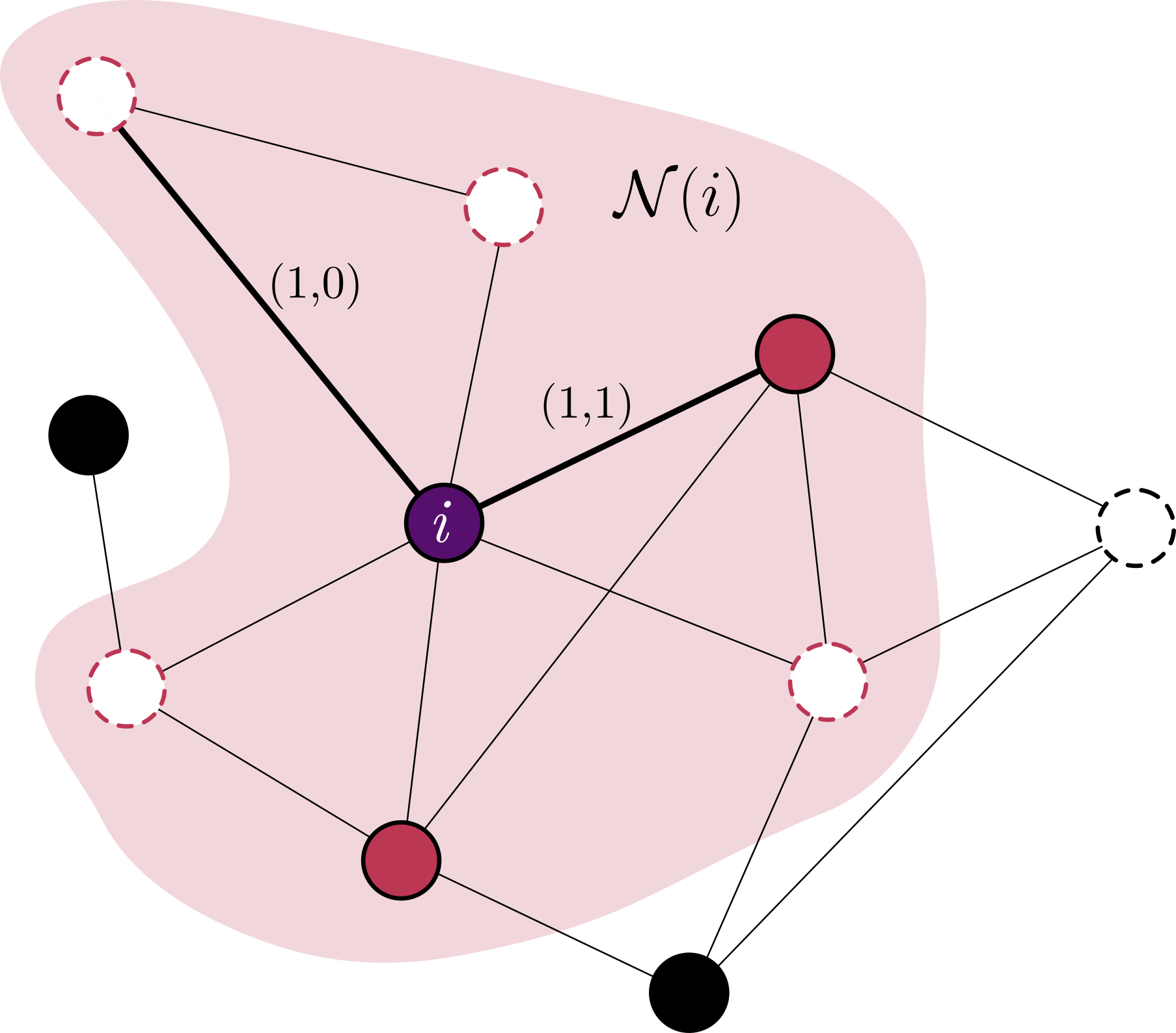
Neighborhood-2

A taxa com a qual pares $(1,1)$ são criados a partir de pares $(1,0)$ tem uma contribuição do sítio já previamente conhecido no estado $1$ $b/z$, mais a contribuição dos demais $z-1$ sítios em $\mathcal{N}(i)$ que estiverem no estado $1$:

\[\begin{align} \nonumber & \frac{b}{z} \rho_{10} \left[ 1 + (z-1) \cdot P(\text{outros sítios ocupados | par (1,0)}) \right] = \\ \nonumber & \frac{b}{z} \rho_{10} \left[ 1 + (z-1) \cdot q_{1|(1,0)} \right] \end{align}\]

Assumindo de forma simplificada que

\[q_{1|(1,0)} = P(\text{outros sítios ocupados | sítio focal = 0}) = q_{1|0}\]

chegamos ao resultado

\[\frac{b}{z}[1 + (z-1)q_{1|0}]\rho_{10}\]

No final das contas estamos assumindo que a informação que um dos vizinhos do sítio focal $0$ é um sítio $1$ não muda de forma significante a probabilidade condicional de que outros sítios na vizinhança esteja ocupada.

Contribuições de morte:

Cada sítio $(1,1)$ morre com uma taxa $(\delta \times \text{vizinhos ocupados} + \gamma)$

Para um sítio $(1,1)$, há com certeza ao menos 1 vizinho ocupado (o outro par), mais $(z-1)q_{1|1}$ outros vizinhos ocupados esperados nos $(z-1)$ vizinhos. Aqui aplicamos a mesma aproximação anterior, de que a probabilidade condicional $q_{1|(1,1)}$ é aproximadamente igual à $q_{1|1}$.

\[[ \delta(1 + (z-1)q_{1|1}) + \gamma]\rho_{11}\] \[\boxed{\frac{1}{2}\frac{d\rho_{11}}{dt} = \frac{b}{z}[1 + (z-1)q_{1|0}]\rho_{10} - [\delta(1 + (z-1)q_{1|1}) + \gamma]\rho_{11}}\]

Equações finais

\[\begin{align} & \frac{d\rho_1}{dt} = bq_{1|0}(1-\rho_1) - (\delta z q_{1|1} + \gamma)\rho_1 \\ & \frac{1}{2}\frac{d\rho_{11}}{dt} = \frac{b}{z}[1 + (z-1)q_{1|0}]\rho_{10} - [\delta(1 + (z-1)q_{1|1}) + \gamma]\rho_{11} \end{align}\]

onde:

Pair Approximation - Modelo Logístico - $\mathcal{N}_c(i) \neq \mathcal{N}_r(i)$

Vejamos agora o caso onde a vizinhança de dispersão para reprodução e a vizinhança de competição não são iguais. Como mencionado anteriormente, este caso é uma formulação mais geral e capaz de incluir o fenômeno de dispersão a longas distâncias. Tipicamente, árvores possuem uma vizinhança de competição limitada pelo alcance de suas raízes [4], porém, a vizinhança de dispersão pode facilmente ser muito maior, chegando a centenas de metros [5].

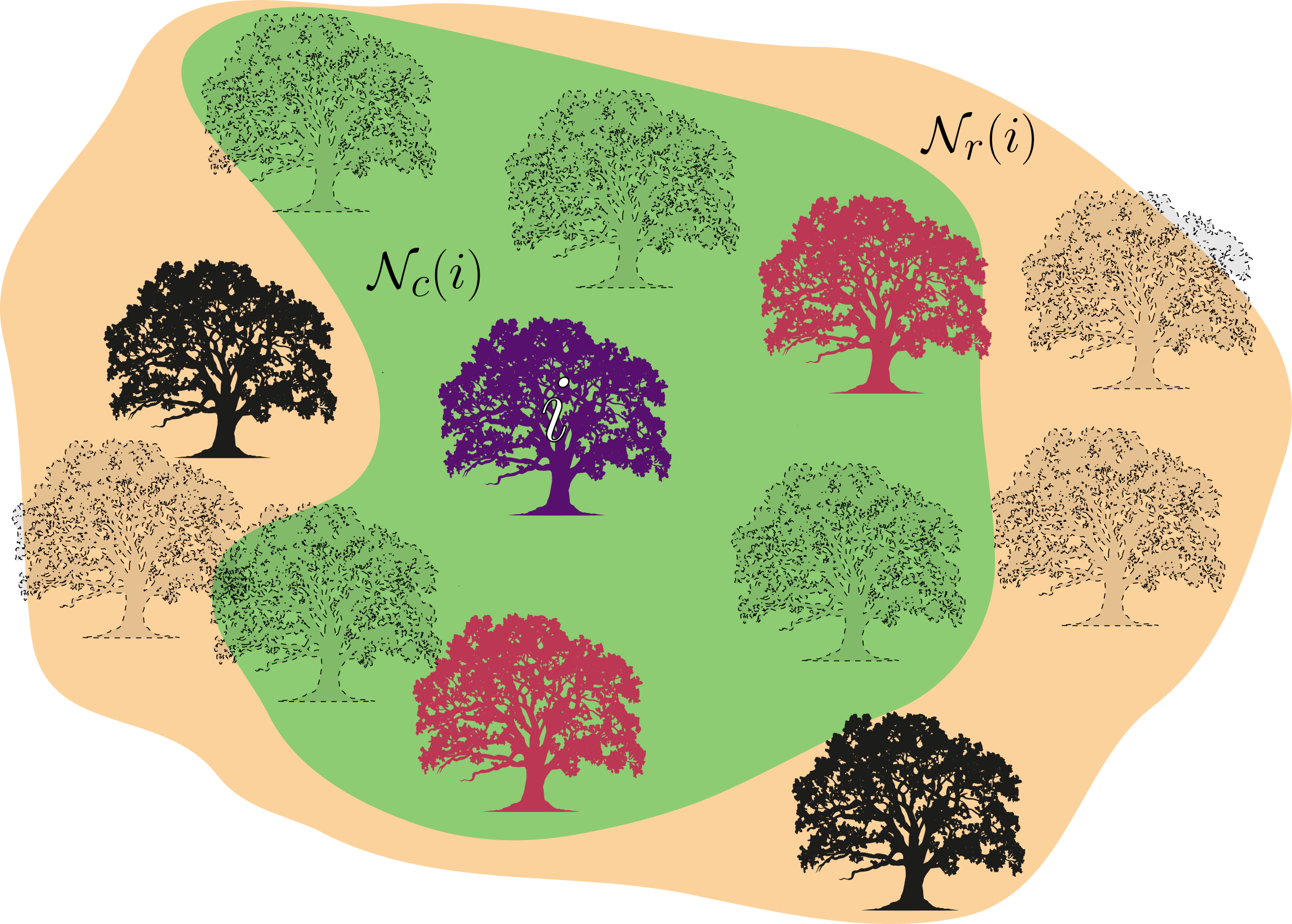
Neighborhood

Agora, a taxa das reações assume a seguinte forma

  1. Nascimento ($0 \to 1$ no sítio $i$):

    \[W(\vec{n} - \hat{e}_i|\vec{n}) = b \sum_{j \in \mathcal{N}_r(i)} n_j \cdot \frac{1}{z} \quad \text{se } n_i = 0\]

  2. Aglomeração ($1 \to 0$ no sítio $i$):

    \[W(\vec{n} + \hat{e}_i|\vec{n}) = \left( \delta \sum_{j \in \mathcal{N}_c(i)} n_j\right) n_i\]

  3. Morte natural ($1 \to 0$ no sítio $i$):

    \[W(\vec{n} + \hat{e}_i|\vec{n}) = \gamma n_i\]

onde aqui faremos $z$ ser o número de sítios na vizinhança de reprodução, e $\tilde{z}$ o número de sítios na vizinhança de competição. Da mesma forma, $\rho$ e $q$ representarão as densidades e probabilidades condicionais de sítios na vizinhança de reprodução $\mathcal{N}_r(i)$, enquanto que $\tilde{\rho}$ e $\tilde{q}$ serão representações das densidades e probabilidades condicionais nos sítios na vizinhança de competição $\mathcal{N}_c(i)$. Como ambas as vizinhanças ainda compartilham a mesma rede, a densidade total de espaços vazios na rede $\rho_0$ e de espaços ocupados $\rho_1$ ainda é a mesma. Isto é:

\[\begin{align} \nonumber & \rho_{00} + \rho_{10} = \tilde{\rho}_{00} + \tilde{\rho}_{10} = \rho_0 \\ \nonumber & \rho_{11} + \rho_{10} = \tilde{\rho}_{11} + \tilde{\rho}_{10} = \rho_1 \end{align}\]

Equação para a média

De forma análoga à como fizemos para o caso de vizinhanças iguais. Calculamos as médias para as taxas de transição das 3 reações possíveis na nossa rede

Contribuição do nascimento:

\[\frac{b}{z} \sum_{j \in \mathcal{N}_r(i)} \langle n_j (1 - n_i) \rangle = \frac{b}{z} \cdot z \cdot \rho_{10} = b q_{1\|0} (1-\rho_1)\]

A taxa de nascimento continua na mesma forma, porém, lembre-se que o $z$ e $\rho_{10}$ aqui não são os mesmos que no caso anterior de vizinhanças iguais. Agora $z$ e $\rho_{10}$ representam a quantidade de sítios e densidade de pares $(1,0)$ dentro da vizinhança de reprodução apenas.

Contribuição da aglomeração:

\[-\left \langle \left(\delta \sum_{j \in \mathcal{N}_c(i)} n_j\right) n_i \right \rangle = -\delta \tilde{z} \tilde{q}_{1|1}\rho_1\]

Contribuição da morte natural:

\[-\gamma \langle n_i \rangle = -\gamma \rho_1\]

portanto:

\[\boxed{\frac{d\rho_1}{dt} = bq_{1|0}(1-\rho_1) - (\delta \tilde{z} \tilde{q}_{1|1} + \gamma)\rho_1}\]

Novamente, encontramos uma equação exata para a densidade de sítios ocupados na rede. Porém, note que agora está equação depende não de $\rho_{11}$, mas sim de $\tilde{\rho}_{11}$. Isso ocorre poís pares do tipo $(1,1)$ dentro da vizinhança de reprodução não possuem nenhum tipo de reação possível, uma vez que a aglomeração só é inclusa dentro da vizinhança de competição. Caso desejássemos incluir efeitos de cooperação, talvez pudéssemos incluir alguma reação benéfica entre sítios $(1,1)$ que percentem a $\mathcal{N}_r(i)$, porém, manteremos as reações simples por hora. Sendo assim, precisamos encontrar a equação diferencial para o par $(1,1)$ na vizinhança de competição.

Derivação da equação do par $\tilde{\rho}_{11}$

Para isso, suponha que um sítio $s_k$ na vizinhança de competição $\mathcal{S}_c(i)$ do indivíduo focal $i$, podem ser ocupados a partir da reprodução de outro indivíduo $j$ cuja vizinhança de reprodução $\mathcal{S}_r(j)$ contém o sítio $s_k$.

Contribuição do nascimento:

Sabemos que cada membro do par $(1,0)$ possui ao menos um sítio ocupado na vizinhança de competição. Já a vizinhança de reprodução é desconhecida. Sendo assim, podemos aproximar a taxa de reprodução por

\[bq_{1|0}\tilde{\rho}_{10}\]

Uma vez que apenas os vizinhos na vizinhança de reprodução irão contribuir para o surgimento de um par $(1,1)$ na vizinhança de competição.

Contribuições de morte:

Cada par $(1,1)$ morre com uma taxa $(\delta \times \text{vizinhos ocupados em }\mathcal{N}_r + \gamma)$

Para um par $(1,1)$, há com certeza ao menos 1 vizinho ocupado (o outro par), mais $(\tilde{z}-1)\tilde{q}{1|1}$ outros vizinhos ocupados esperados nos $(\tilde{z}-1)$ vizinhos. Aqui aplicamos a mesma aproximação anterior, de que a probabilidade condicional $\tilde{q}{1|(1,1)}$ é aproximadamente igual à $\tilde{q}_{1|1}$, ignorando a informação já conhecida a respeito de ao menos um sítio ocupado na vizinhança do sítio focal.

\[[\delta(1 + (\tilde{z}-1)\tilde{q}_{1|1}) + \gamma]\tilde{\rho}_{11}\]

A equação final para $\tilde{\rho}_{11}$ assume a forma:

\[\boxed{\frac{1}{2}\frac{d\tilde{\rho}_{11}}{dt} = bq_{1|0}\tilde{\rho}_{10} - [ \delta(1 + (\tilde{z}-1)\tilde{q}_{1|1}) + \gamma]\tilde{\rho}_{11}}\]

Equações finais

\[\begin{align} & \frac{d\rho_1}{dt} = bq_{1|0}(1-\rho_1) - (\delta \tilde{z} \tilde{q}_{1|1} + \gamma)\rho_1 \\ & \frac{1}{2}\frac{d\tilde{\rho}_{11}}{dt} = b q_{1|0}\tilde{\rho}_{10} - [\delta(1 + (\tilde{z}-1)\tilde{q}_{1|1}) + \gamma]\tilde{\rho}_{11} \end{align}\]

Pair Approximation - Competição entre espécies $\mathcal{N}_c^\mu(i) = \mathcal{N}_r^\mu(i)$ e $\left( \mathcal{N}_c^1, \mathcal{N}_r^1 \right) \neq \left( \mathcal{N}_c^2, \mathcal{N}_r^2 \right)$

Descrição do sistema

É hora de dar um passo adiante. Estamos aptos a considerar um sistema com duas populações diferentes que compartilham o mesmo habitat (sendo o habitat definido pela rede de sítios). Estas duas populações podem representar duas espécies diferentes ou dois conjuntos de espécies que pertencem a grupos filogenéticos diferentes, por exemplo. Por simplicidade, vamos considerar que cada população representa uma espécie de planta. Dessa forma, temos sítios por nossa rede que podem estar vazios $(0)$, ocupados pela espécie $(1)$ ou ocupados pela espécie $(2)$.

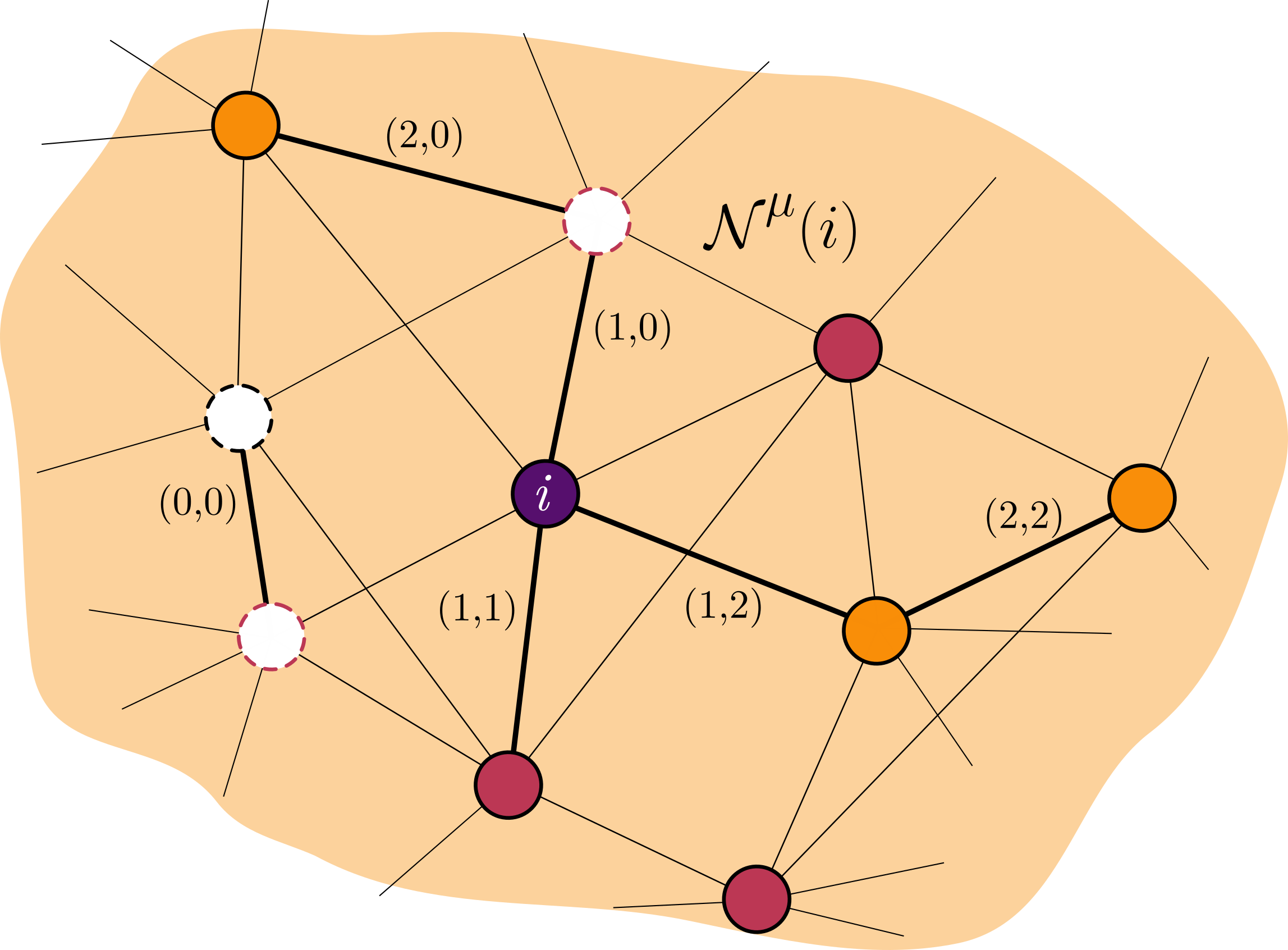
Neighborhood

Na figura acima, sítios laranjas são sítios ocupados pela espécie $2$, e os sítios avermelhados são ocupados pela espécie $1$. O sítio roxo é o sítio focal, pertencente à espécie $1$ e os brancos são sítios vazios. Note que agora há 6 tipos diferentes de conexões entre vizinhos:

  1. Espécie $\mu$ com um sítio vazio $(\mu,0)$ (2 possibilidades diferentes - (1,0) e (2,0))
  2. Espécie $\mu$ com um sítio da mesma espécie $\mu$ $(\mu,\mu)$ (2 possibilidades diferentes - (1,1) e (2,2))
  3. Espécie $\mu$ com um sítio de outra espécie $\eta$ $(\mu,\eta)$ (uma única possibilidade - (1,2))
  4. Um sítio vazio com outro sítio vazio $(0,0)$

Assim, podemos descrever o estado do sistema de duas formas diferentes. Na primeira, representamos um vetor $\vec{n}$ com entradas $0,1,2$, de forma similar ao caso com uma única espécie. Ou podemos representar uma matriz de tamanho $N \times s$, onde $N$ é o número total de sítios na rede e $s$ é o número de espécies. Cada linha $i$ representa em a qual espécie pertence o ocupante do $i$-ésimo sítio. Por exemplo, a matriz de estado $\mathbf{n}$

\[\begin{align} \mathbf{n} = \begin{pmatrix} 0 & 1 \\ 0 & 0 \\ 1 & 0 \\ 0 & 1 \end{pmatrix} \end{align}\]

nos diz que o primeiro e o último sítios da rede são ocupados por indivíduos da espécie 2, o segundo sítio está vazio e o 3ª sítio está ocupado por um indivíduo da espécie 1.

Daqui em diante, usaremos as letras gregas $(\mu,\eta)$ para se referir de forma genérica as espécies e as letras latinas $(i,j,k)$ para se referir aos sítios da rede, e trataremos $\mathcal{N}_c^\mu(i) = \mathcal{N}_r^\mu(i) = \mathcal{N}^\mu(i)$ para iniciar com simplicidade.

Como sempre, é útil trazer uma interpretação física/biológica para esta descrição abstrata. A imagem abaixo ilustra um cenário ecológico descrito pelo sistema acima. Neste caso, como ambas as espécies de árvores ilustradas são diferentes, as vizinhanças de reprodução e competição podem diferir entre as espécies, dado que cada uma pode ter estratégias de reprodução diferentes e captação e uso de recursos do solo, do ar e de luz diferentes. Ainda mais, podemos tornar a taxa de reprodução de cada espécie como uma função que dependa da distância entre sítios dentro da vizinhança de reprodução $b_\mu = b_\mu(r_{ij})$ [EXPLORAR ISSO DEPOIS E SE DER CERTO SÓ].

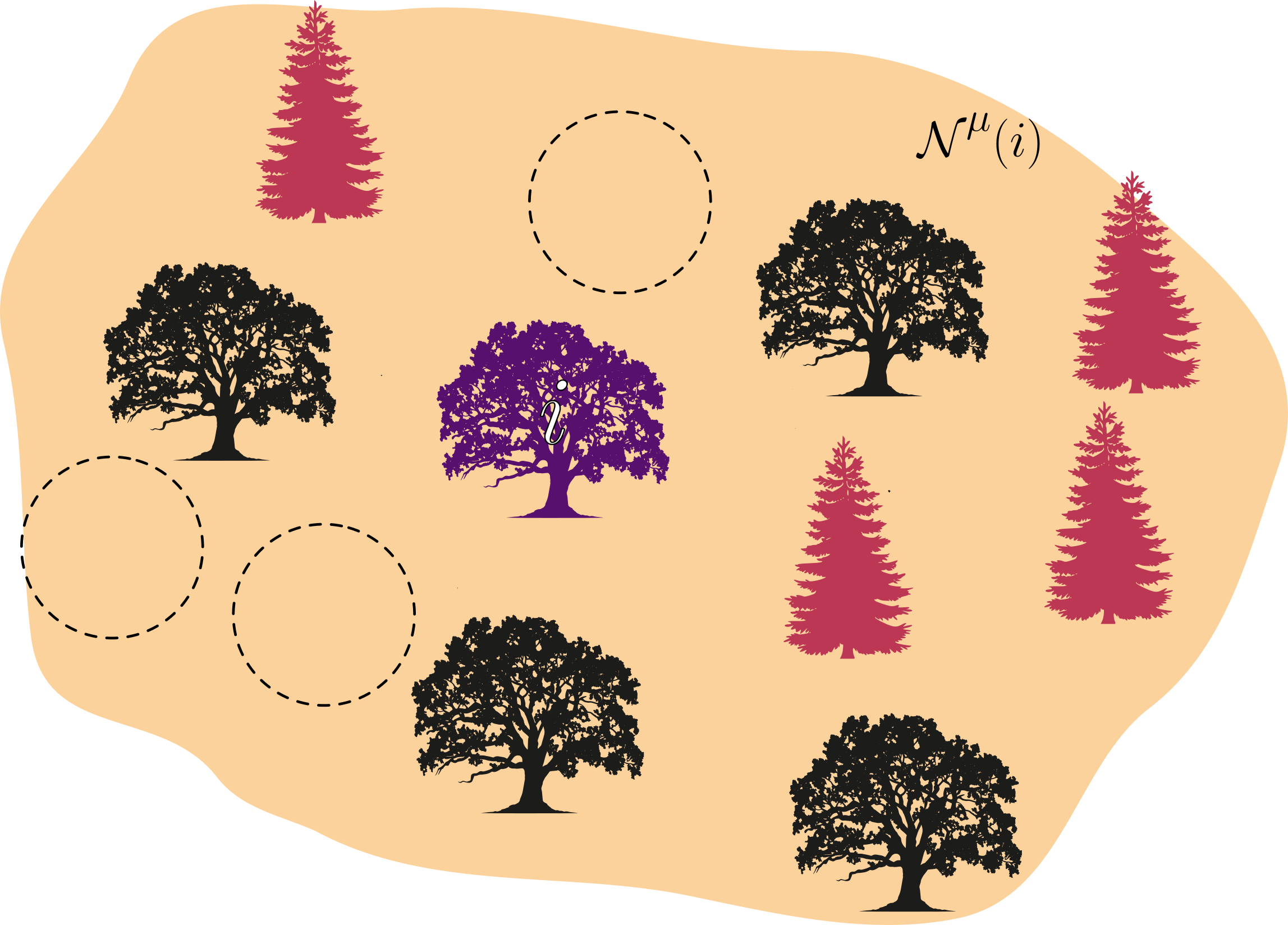
Neighborhood

De forma análoga ao caso logístico, definimos as taxas para as reações possíveis, que aumentam de 3 para 4:

Reações:

  1. Nasicmento: A espécie $\mu$ se reproduz gerando descendentes a uma taxa $b_\mu$, que é dispersada aleatoriamente para um dos $z^\mu$ sítios em sua vizinhança de reprodução $\mathcal{N}^\mu(i)$.

  2. Morte natural: Indivíduos da espécie $\mu$ morrem de forma natural a uma taxa $\gamma_\mu$.

  3. Aglomeração: Indivíduos ainda morrem devido à aglomeração com outros indivíduos da mesma espécie, com uma taxa $\sigma_{\mu \mu} \times$ (nº de vizinhos da espécie $\mu$ na vizinhança de competição $\mathcal{N}^\mu(i)$).

  4. Competição interespecífica: Sítios ocupados pela espécie $\mu$ morrem devido à competição por recursos com a espécie $\eta$ a uma taxa $\sigma_{\mu \eta} \times$ (n° de vizinhos da espécie $\eta$ na vizinhança de competição $\mathcal{N}^\mu(i)$).

A partir de agora, mudamos a representação do termo de competição de $\delta$ para $\sigma$. $\sigma$ é agora uma matriz de interação que define os coeficientes das taxas de competição inter e intraespecífica entre as espécies $\mu$ e $\eta$.

\[\begin{align} \sigma = \begin{pmatrix} \sigma_{\mu \mu} & \sigma_{\mu \eta} \\ \sigma_{\eta \mu} & \sigma_{\eta \eta} \end{pmatrix} \end{align}\]

onde $\sigma_{\mu \eta} \neq \sigma_{\eta \mu}$, poís uma espécie pode ser mais afetada pela presença de outra. Antes de continuar, agora que temos duas espécies, vamos rever as definições antes mostradas para o caso logístico:

Densidades:

Densidade de pares:

Probabilidades:

Equação mestra e taxas

Sendo $P(\vec{n}, t)$ a probabilidade de o sistema se encontrar na configuração $\vec{n} = (n_1, n_2, \ldots, n_N)$ no instante $t$, onde $n_i \in {0,1,2}$ é o estado do sítio $i$. A equação mestra do sistema é dada em termos das taxas de transição:

\[\frac{dP(\vec{n}, t)}{dt} = \sum_{\vec{n}'} [W(\vec{n}|\vec{n}') P(\vec{n}', t) - W(\vec{n}'|\vec{n}) P(\vec{n}, t)]\]

Taxas de transição $W(\vec{n}’|\vec{n})$:

  1. Nascimento ($0 \to \mu$ no sítio $i$): O nascimento se da da mesma forma que no caso logístico. Cada vizinho ocupado pela espécie $\mu$ na vizinhança de reprodução do sítio $i$ irá tentar ocupar o sítio com um descendente a uma taxa $b_\mu$

    \[W(\vec{n} + \mu\hat{e}_i|\vec{n}) = b_\mu \sum_{j \in \mathcal{N}^\mu(i)} \delta_{n_j,\mu} \quad \text{se } n_i = 0\]

  2. Morte ($\mu \to 0$ no sítio $i$): Há três contribuições para a taxa total de morte. A morte natural e independente de vizinhos, a morte por competição interspecífica e a morte por competição intraespecífica

    \[W(\vec{n} - \mu\hat{e}_i|\vec{n}) = \left[\gamma_\mu + \sigma_{\mu \mu} \sum_{j \in \mathcal{N}^\mu(i)} \delta_{n_j,\mu} + \sigma_{\mu \eta} \sum_{j \in \vec{N}_c^\mu(i)} \delta_{n_j,\eta} \right] \delta_{n_i, \mu}\]

Onde

$$ \delta_{n_j,\mu} = \begin{cases} 0, \, \text{se } n_j \neq \mu
1, \, \text{se } n_j = \mu \end{cases}

$$ é a delta de dirac, assumindo o valor 1 sempre que $n_j = \mu$ e 0 caso contrário.

Equações de densidades

Para a densidade de sítios ocupados pela espécie $\mu$:

\[\frac{d\rho_\mu}{dt} = \left \langle \frac{d}{dt} \sum_i \mathbf{1}_{n_i = \mu} \right \rangle\]

Contribuição do nascimento:

Cada sítio vazio recebe um filhote a uma taxa:

\[b_\mu \sum_{j \in \mathcal{N}^\mu(i)} \mathbf{1}_{n_j = \mu} = b_\mu \times z_\mu \times P(\text{vizinho é $\mu$ | sítio é 0}) = b_\mu z_\mu q_{\mu|0}\]

Taxa total de nascimentos: $b_\mu z_\mu q_{\mu|0} \rho_0 = b_\mu z_\mu q_{\mu|0}(1 - \rho_\mu - \rho_\eta)$

Contribuição da morte:

Portanto:

\[\begin{align} \boxed{\frac{d\rho_\mu}{dt} = b_\mu z_\mu q_{\mu|0}(1 - \rho_\mu - \rho_\eta) - (\gamma_\mu + \sigma_{\mu \mu} z_\mu q_{\mu|\mu} + \sigma_{\mu \eta} z_\mu q_{\eta|\mu})\rho_\mu} \end{align}\]

Equações para os pares

Já vimos que possuímos as seguintes densidades de pares: $\rho_{11}$, $\rho_{22}$, $\rho_{12}$, $\rho_{01}$, $\rho_{02}$, $\rho_{00}$. Felizmente, devido aos vínculos do nosso sistema

\[\rho_{\mu 0} = \rho_{\mu} - \rho_{\mu \mu} - \rho_{\mu \eta}\]

e

\[\rho_{00} = \rho_0 - \rho_{01} - \rho_{02}\]

Pares intraespecíficos: $\rho_{\mu \mu}$

\[\frac{1}{2}\frac{d\rho_{\mu \mu}}{dt} = \text{Taxa de nascimento criando pares }(\mu, \mu) - \text{Taxa de mortalidade eliminando pares} (\mu, \mu)\]

Contribuições do nascimento: Um par do tipo $(\mu, 0)$ se torna $(\mu, \mu)$ quando a espécie $\mu$ ocupar um sítio vazio na vizinhança do sítio focal $\mu$

\[b_\mu [1 + (z_\mu-1)q_{\mu|0}] \rho_{0\mu}\]

Contribuições da morte: Cada sítio $(\mu,\mu)$ se desfaz com uma taxa dada pela mortalidade de um sítio $\mu$

\[\gamma_\mu + \sigma_{\mu \mu}[1 + (z_\mu-1)q_{\mu|\mu}] + \sigma_{\mu \eta}(z_\mu-1)q_{\eta|\mu}\]

Portanto:

\[\begin{align} \boxed{\frac{1}{2}\frac{d\rho_{\mu \mu}}{dt} = b_\mu[1 + (z_\mu-1)q_{\mu|0}]\rho_{0\mu} - [\gamma_\mu + \sigma_{\mu \mu}(1 + (z_\mu-1)q_{\mu|\mu}) + \sigma_{\mu \eta}(z_\mu-1)q_{\eta|\mu}]\rho_{\mu \mu}} \end{align}\]

Par interespecífico: $\rho_{\mu \eta}$

Contribuição de nascimento: Um par $(\mu,0)$ se torna um par $(\mu,\eta)$ quando a espécie $\eta$ der origem a um novo indivíduo no sítio vazio na vizinhança de $\mu$: $b_\eta(z_\eta-1)q_{\eta|0}\rho_{0\mu}$. Da mesma forma, um par $(0,\eta)$ se torna um par $(\mu, \eta)$ quando um indivíduo da espécie $\mu$ se reproduzir gerando um novo ocupante na vizinhança do sítio focal da espécie $\eta$: $b_\mu(z_\mu-1)q_{\mu|0}\rho_{0\eta}$. Note que aqui não termos o termo $1 + \cdots$ que nem nos pares intraespecíficos, pois o vizinho já conhecido na vizinhança do espaço vazio percente a outra espécie, e portanto não contribui para o nascimento de um indivíduo da espécie focal.

Contribuição da morte: Um sítio da espécie $\mu$ se torna desocupado ao morrer com taxa: $[\gamma_\mu + \sigma_{\mu \mu}(z_\mu-1)q_{\mu|\mu} + \sigma_{\mu \eta}(1 + (z_\mu-1)q_{\eta|\mu})]\rho_{\mu \eta}$. Além disso, um sítio da espécie $\eta$ se torna desocupado com taxa: $[\gamma_\eta + \sigma_{\eta \eta}(z_\eta-1)q_{\eta|\eta} + \sigma_{\eta \mu}(1 + (z_\eta-1)q_{\mu|\eta})]\rho_{\mu \eta}$

Assim, acabamos com:

\[\begin{align} \nonumber \frac{d\rho_{\mu \eta}}{dt} & = b_\mu (z_\mu-1)q_{\mu|0}\rho_{0\eta} + b_\eta (z_\eta-1)q_{\eta|0}\rho_{0\mu} \\ & - [\gamma_\mu + \sigma_{\mu \mu}(z_\mu-1)q_{\mu|\mu} + \sigma_{\mu \eta}(1 + (z_\mu-1)q_{\eta|\mu})] \rho_{\mu \eta} \\ \nonumber & - [\gamma_\eta + \sigma_{\eta \eta}(z_\eta-1)q_{\eta|\eta} + \sigma_{\eta \mu}(1 + (z_\eta-1)q_{\mu|\eta})] \rho_{\mu \eta} \end{align}\]

Equações finais

\[\begin{align} & \frac{d\rho_1}{dt} = b_1 z_1 q_{1|0}(1 - \rho_1 - \rho_2) - (\gamma_1 + \sigma_{11} z_1 q_{1|1} + \sigma_{12} z_1 q_{2|1})\rho_1 \\ & \frac{d\rho_2}{dt} = b_2 z_2 q_{2|0}(1 - \rho_1 - \rho_2) - (\gamma_2 + \sigma_{22} z_2 q_{2|2} + \sigma_{21} z_2 q_{1|2})\rho_2 \\ & \frac{1}{2}\frac{d\rho_{11}}{dt} = b_1[1 + (z_1-1)q_{1|0}]\rho_{01} - [\gamma_1 + \sigma_{11}(1 + (z_1-1)q_{1|1}) + \sigma_{12}(z_1-1)q_{2|1}]\rho_{11} \\ & \frac{1}{2}\frac{d\rho_{22}}{dt} = b_2[1 + (z_2-1)q_{2|0}]\rho_{02} - [\gamma_2 + \sigma_{22}(1 + (z_2-1)q_{2|2}) + \sigma_{21}(z_2-1)q_{1|2}]\rho_{22} \\ \nonumber & \frac{d\rho_{1 2}}{dt} = b_1(z_1-1)q_{1|0}\rho_{20} + b_2(z_2-1)q_{2|0}\rho_{10} \\ & - [\gamma_1 + \sigma_{1 1}(z_1-1)q_{1|1} + \sigma_{1 2}(1 + (z_1-1)q_{2|1})] \rho_{1 2} \\ \nonumber & - [\gamma_2 + \sigma_{2 2}(z_2-1)q_{2|2} + \sigma_{2 1}(1 + (z_2-1)q_{1|2})] \rho_{1 2} \end{align}\]

Explicitando os termos de probabilidades condicionais, chegamos a

\[\begin{align} & \frac{d\rho_1}{dt} = b_1 z_1 \rho_{10} - \gamma_1 \rho_1 - \sigma_{11} z_1 \rho_{11} - \sigma_{12} z_1 \rho_{12} \\ & \frac{d\rho_2}{dt} = b_2 z_2 \rho_{20} - \gamma_2 \rho_2 - \sigma_{22} z_2 \rho_{22} - \sigma_{21} z_2 \rho_{12} \\ & \frac{1}{2}\frac{d\rho_{11}}{dt} = b_1 \left[\rho_{10} + z_1 \frac{\rho_{10}^2}{\rho_0} - \frac{\rho_{10}^2}{\rho_0} \right] - \left[\gamma_1 \rho_{11} + \sigma_{11} \left(\rho_{11} + z_1 \frac{\rho_{11}^2}{\rho_1}-\frac{\rho_{11}^2}{\rho_1} \right) + \right. \\ \nonumber & \left. + \sigma_{12}(z_1-1)\frac{\rho_{12} \rho_{11}}{\rho_1} \right] \\ & \frac{1}{2}\frac{d\rho_{22}}{dt} = b_2 \left[\rho_{20} + z_2 \frac{\rho_{20}^2}{\rho_0} - \frac{\rho_{20}^2}{\rho_0} \right] - \left[\gamma_2 \rho_{22} + \sigma_{22} \left(\rho_{22} + z_2 \frac{\rho_{22}^2}{\rho_2}-\frac{\rho_{22}^2}{\rho_2} \right) + \right. \\ \nonumber & \left. + \sigma_{21}(z_2-1)\frac{\rho_{12} \rho_{22}}{\rho_2} \right] \\ & \frac{d\rho_{12}}{dt} = b_1 (z_1 -1)\frac{\rho_{10} \rho_{20}}{\rho_0} + b_2 (z_2 - 1)\frac{\rho_{20} \rho_{10}}{\rho_0} - \\ & - \left[\gamma_1 \rho_{12} + \sigma_{11}(z_1-1)\frac{\rho_{11} \rho_{12}}{\rho_1} + \sigma_{12}\left(1 + (z_1-1)\frac{\rho_{12}^2}{\rho_1} \right) \right] - \\ & - \left[\gamma_2 \rho_{12} + \sigma_{22}(z_2-1)\frac{\rho_{22} \rho_{12}}{\rho_2} + \sigma_{21} \left(1 + (z_2-1)\frac{\rho_{12}^2}{\rho_2} \right) \right] \end{align}\]

Referências

  1. Ellner, S. P. (2001). Pair Approximation for Lattice Models with Multiple Interaction Scales. Journal of Theoretical Biology, v 210, p 435-447. doi.org/10.1006/jtbi.2001.2322

  2. Hopcraft, J. G. C., Anderson, T. M., Pérez‐Vila, S., Mayemba, E., & Olff, H. (2012). Body size and the division of niche space: food and predation differentially shape the distribution of Serengeti grazers. Journal of Animal Ecology, 81(1), 201-213. doi.org/10.1111/j.1365-2656.2011.01885.x

  3. Owen‐Smith, N., & Mills, M. G. L. (2008). Predator–prey size relationships in an African large‐mammal food web. Journal of Animal Ecology, 77(1), 173-183. doi.org/10.1111/j.1365-2656.2007.01314.x

  4. Cabal, C., Martínez-García, R., de Castro Aguilar, A., Valladares, F., & Pacala, S. W. (2020). The exploitative segregation of plant roots. Science, 370(6521), 1197-1199. doi.org/10.1126/science.aba9877

  5. Hewitt, N., & Kellman, M. (2002). Tree seed dispersal among forest fragments: II. Dispersal abilities and biogeographical controls. Journal of Biogeography, 29(3), 351-363. doi.org/10.1046/j.1365-2699.2002.00679.x