Pedro Cintra

🦆 Meu site pessoal

:thinking: Vacinados morrem mais?

Já em Maio de 2021, poucos meses após o inicio da vacinação contra a COVID-19 no Brasil, começamos a ver algumas matérias comentando sobre o aumento de casos e óbitos em idosos vacinados. Imediatamente isso gera preocupação e duvidas. Se a vacina funciona, então porque a maior parte dos casos estão ocorrendo naqueles que se vacinaram?

Acontece que isso é normal, inclusive esperado, e não mostra nenhuma ineficácia na proteção das vacinas. Como nenhuma vacina tem 100% de eficácia, é normal que algumas pessoas sejam infectadas mesmo vacinadas, as chamadas breakthrough infections em inglês. Se minha vacina tem uma eficácia de 90%, após eu vacinar 100 pessoas, 10 delas ainda vão poder ser infectadas mesmo vacinadas. Agora, se eu vacinar 200 pessoas, 20 delas podem ser infectadas ainda. Ou seja, quanto mais pessoas eu vacino, mais casos entre os vacinados eu vou ver. Se eu vacinar a população inteira, 100% dos casos vão ser infecções breakthrough. Portanto, ver notícias como “O numero de casos entre os vacinados aumentou” é apenas consequência de estarmos vacinando mais pessoas (e protegendo mais também).

Imaginem um cenário lindo onde 100% da população está vacinada com uma vacina 99.99% eficaz em prevenir óbitos. É claro que, já que a vacina não é 100% eficaz, e todo mundo ta vacinado, todos os óbitos vistos serão em vacinados, apesar de serem MUITO menores.

Podemos inclusive descrever o quanto casos/hospitalizações/óbitos de breakthrough (aqueles que afetam pessoas já vacinadas) vão representar do total de casos/hospitalizações/óbitos quantitativamente. Para isso, irei mostrar aqui uma descrição matemática da relação entre óbitos breakthrough e a fração de pessoas vacinadas. Isso depende principalmente da % de pessoas já vacinadas $\left( f_v \right)$ e da efetividade $\left( V_E \right)$ da vacina em prevenir o desfecho específico (neste caso, óbitos)

\[\begin{equation} B\left(f_{v}|V_{E} \right) = \frac{f_{v} \left(1 - V_E \right)}{f_v \left(1 - V_E \right) + \left(1 - f_v \right)} \end{equation}\]

esta equação nos premite relacionar a fração de pessoas vacinadas, representada por $f_v$, a efetividade do programa de vacinação $V_E$ com a fração de óbitos breakthrough $B$. A efetividade do programa de vacinação depende de diversas características como a eficácia das vacinas em uso, comportamento social dos vacinados e a distribuição da aplicação das vacinas em faixas etárias diferentes. Podemos representar isso, de uma forma simples como

\[\begin{equation} V_E = \frac{1}{d_v} \sum_{j=1}^M \sum_{i=1}^N w_{ij} p_{ij} \end{equation}\]

sendo $d_v$ a disposição de vacinados a se exporem ao vírus, em comparação a não vacinados, $w_{ij}$ é a prevalência de uso da $i$-ésima vacina na faixa etária $j$, $p_{ij}$ é a eficácia da $i$-ésima vacina na faixa etária $j$. Apesar de assustadora para muitos, não precisaremos nos preocupar com esta equação para entender a relação quantitativa entre óbitos breakthrough e vacinados, felizmente a efetividade do programa de vacinação já é calculada em estudos científicos e monitoramento epidemiológico, deixo alguns no fim deste post.

Dependendo da efetividade da vacinação, que por si depende da eficácia, da exposição dos vacinados e das vacinas utilizadas, essa relação de prevalência de breakthroughs nos desfechos e vacinação anda de formas diferentes.

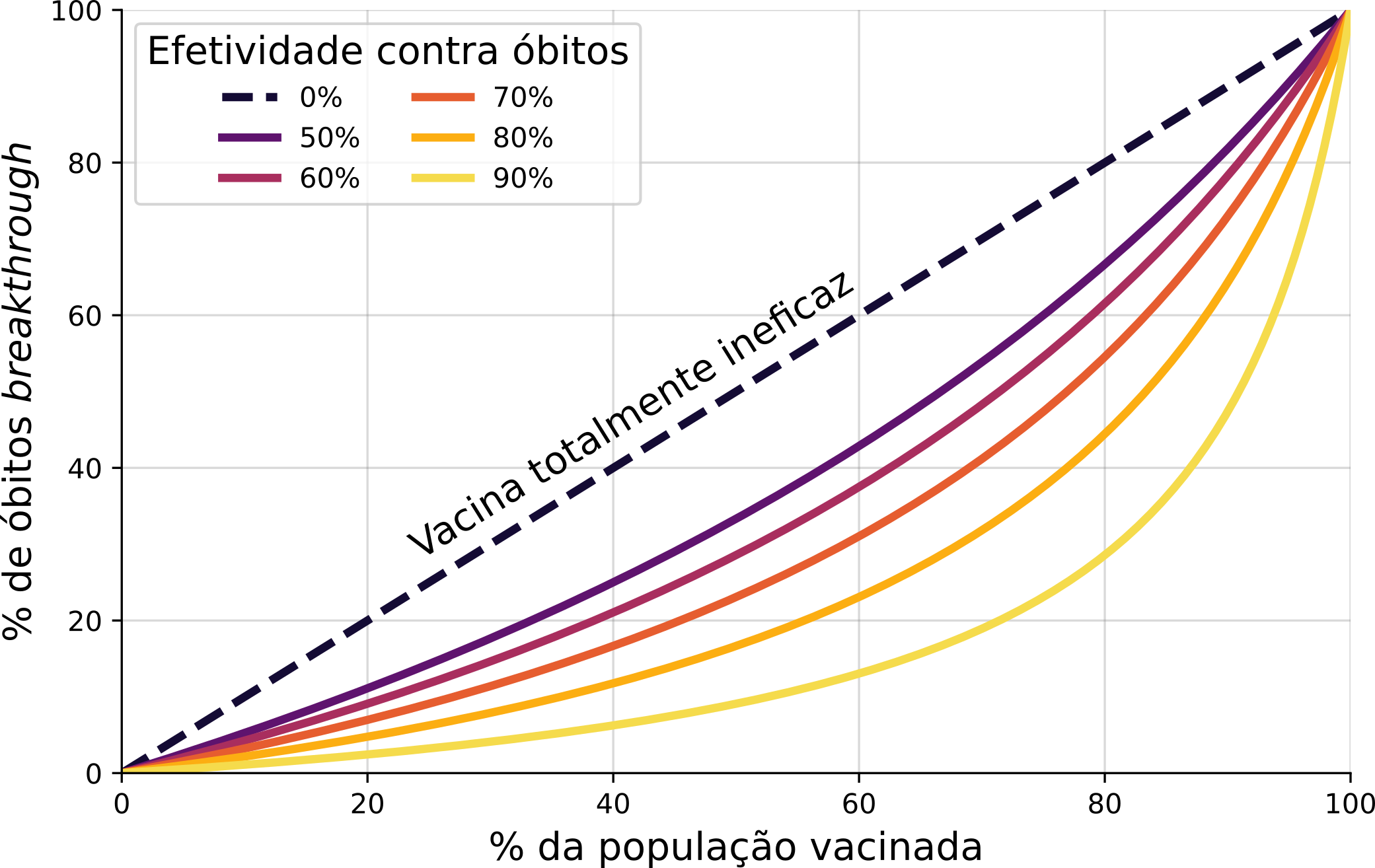
breakthroug_infections

Vamos dar atenção a este gráfico por um tempo. Primeiro, é bom notar como a relação entre a população vacinada e os óbitos breakthrough não é linear (exceto no caso em que a vacina é ineficaz). Segundo, quanto mais eficaz a vacina é, mais gente precisa estar vacinada para vermos um aumento rápido na porcentagem de óbitos breakthrough. O que esse gráfico NÃO MOSTRA é que o numero total de desfechos (casos/hosp/óbitos) será muito menor. Esse gráfico mostra a proporção nos desfechos, não o total.

Ohemos para um caso real, acredito que isso ajude a deixar mais claro. No Estados Unidos o CDC divulga relatórios de mortalidade e vacinação, durante o período de Março de 2021 a Janeiro de 2022, o programa de vacinação no país atingiu uma efetividade contra óbitos em torno de 94%, com uma margem de confiança de 95% entre 91 e 96%. Isso significa que poderíamos esperar um comportamento como esse

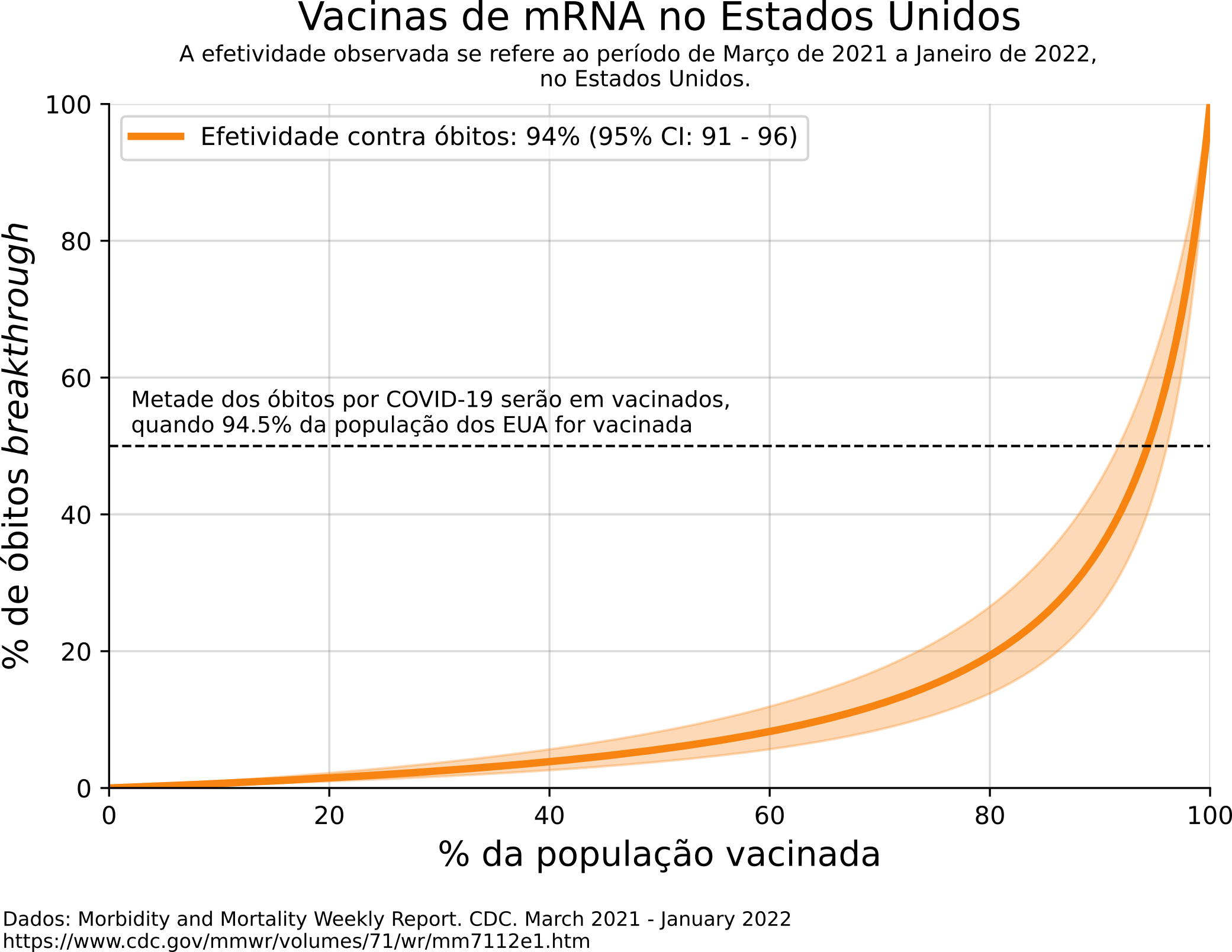
breakthroug_infections_mRNA

Dessa forma, podemos esperar que quando perto de 94% da população americana estivesse totalmente vacinada, metade dos óbitos por COVID-19 ocorreriam em vacinados. Novamente, este número seria muito pequeno. Imagine só, se temos este cenário e durante um ano apenas dois óbitos por COVID-19 ocorrem, um em uma pessoa vacinada e outro em uma pessoa não vacinada, seriam exatamente 50% de óbitos breakthrough. Porém, o numero total de óbitos seria muito pequeno.

Atenção à limitações

Desenvolvi tudo isso para explicar o porque que óbitos ou infecções em vacinados aumentar, em relação aos não vacinados, é algo esperado e na verdade não indica problemas com vacinas. Isso NÃO É um modelo científico capaz de prever com exatidão a relação entre vacinados e óbitos breakthrough.

Há muitos fatores que aqui foram excluídos, por simplicidade e para dar mais foco na natureza do efeito da vacinação, como o surgimento de novas variantes, a perda de imunidade com o tempo e comportamentos sociais que possam tornar as pessoas mais expostas ao vírus. Tudo isso muda esta relação. Meu ponto aqui é mostrar que mesmo sem essas coisas, é natural que essa proporção de óbitos tenda mais para o lado dos vacinados, uma vez que a vacinação abrange mais pessoas.

Alguns artigos de avaliação de efetividade de vacinação

Data: 10/03/2024